在介绍Vigenere密码之前,先介绍一个更为简单的密码系统:凯撒密码(Caeser Cipher)。据称,当年凯撒曾用这种方法和手下的将领进行通信,传达指挥命令。凯撒密码是一种替换加密技术,即明文中所有字母都在字母表上向后或者向前偏移一个固定的距离,被替换成密文。当这个距离是3的时候,即称作凯撒密码。
凯撒密码
凯撒密码的加密、解密可以通过取模的加减法进行计算。首先将字母用数字替代 A = 0,B = 1, …, Z = 25。 当偏移量为n的时候加密方法是 $$ c = m + n \mod 26,$$ 解密方法是$$ m = c - n \mod 26。$$ 当n = 3时,得到
明文字母表: ABCDEFGHIJKLMNOPQRSTUVWXYZ
密文字母表: DEFGHIJKLMNOPQRSTUVWXYZABC
使用时,加密者查找明文字母表中需要加密的消息中的每一个字母所在位置,并且写下密文字母表中对应的字母。需要解密的人则根据事先已知的密钥反过来操作,得到原来的明文。例如:
明文: THE QUICK BROWN FOX JUMPS OVER THE LAZY DOG
密文: WKH TXLFN EURZQ IRA MXPSV RYHU WKH ODCB GRJ
通过上面的描述可以知道,凯撒密码里最关键的信息是事先约定好的偏移量n,也被称作密钥。同时也很容易发现,凯撒密码有些缺陷,因为密钥空间太小很容易被暴力破解。另外一个缺陷就是替换过后的字母唯一,即A替换以后的密文只能是某一个字母,比如D。通过大量统计,人们发现了英语文本里面每个字母出现的频率接近某个固定的概率,比如E是出现频率最高的一个字母。只要攻击者拿到大量的密文,然后统计其中出现次数最多的字母,即可认为其对应的明文是E,从而解出密钥。
Vigenere密码

上图被称作Vigenere Square,展示了所有可能的凯撒密码。在凯撒密码中,一次加密只会用到一个密钥,导致相同密文对应的明文总相同。所以,有人根据凯撒密码发明了Vigenere密码:不同位置的明文用不同的密钥进行加密,因此相同字母由于使用不同的密钥而被替换成不同的密文, 不同字母也可能因为使用不同的密钥而被替换成相同的密文。在下面的例子里我们选择LEMON作为密钥的话,观察明文中的T和密文中的R可以验证前述说法。
明文: ATTACK AT DAWN
密钥: LEMONL EM ONLE
密文: LXFOPV EF RNHR
这样,直接统计密文中的字符频率便失去了作用。那么这种情况该怎么办呢?其实用心思考一下可以发现,破解Vigenere密码的关键是密钥的长度。因为相隔一个密钥长度的明文都使用同一个密钥进行加密,只要攻击者找到了密钥的长度,那么剩下的工作便是分别破解若干个密文的子序列,也就是破解凯撒密码。现在的问题在于如何获得密钥的长度呢?答案是:猜。
自相关系数
假设密钥的长度是d,文本的长度为l。可以认为d可能的取值范围是[1,l],但基于习惯的考虑,可以将d缩小在合适的数值之内,比如200。接下来介绍一种自相关系数,来帮助我们猜出d。
$$ AutoCor(d) = \sum_{i=0}^{l-d} <a_i, a_{i+d}> $$
\(a_i\)和\(a_{i+d}\)是相距d的两个字母,如果它们相同,则<\(a_i, a_{i+d}\)>为0,否则为1。尝试计算从d=1到d=200的自相关系数,然后在二维座标系里绘制出(d,AutoCor(d))的点图。然后根据图中极小值出现的位置,判断出d的取值。 下面是计算每一个自相关系数的代码片段
static double AutoCorrelation (int d)
{
int autoCor = 0;
for (size_t i = 0; i <= (TextLength-d); i++)
{
if(TextArray[i] != TextArray[i+d]){
autoCor = autoCor + 1;
}
}
return autoCor;
}应该很多人好奇,为什么这样的计算就可以得到d?现在我们再来认真回顾一下Vigenere密码加密的过程:通过重复使用密钥,得到了一个和明文序列一样长度的密钥序列,在这个序列里面,每隔d个距离便是相同的子密钥单元,比如上面例子当中每隔5个距离又出现的L, E, M, O, N。加密过程如下所示
$$ c_i = m_i + k_{i \mod d} \mod 26。$$
可以想象这样的一个情况,假如相邻d个距离的明文恰好也一样,那么二者替换过后的密文也相同。而这种情况出现的概率不出意外应该远远小于二者不同的情况,也就是说当d的取值恰为密钥长度或者是密钥长度倍数的时候,统计出来AutoCor(d)的值要显著小于其它情况。根据出现的第一个极小值,攻击者可以推测出密钥长度。那么,接下来的工作比较简单了,就是分别解出每一个子密钥。
字母频率
在数学家没有找到日常英语文本里面字母的分布频率之前,求解凯撒密码可以通过暴力穷举,因为密钥空间只有26个元素。后来统计学家通过大量的文本统计发现了字母的分布频率,例如下表P
| 字母 | 频率 | 字母 | 频率 |
|---|---|---|---|
| A | 0.0710223 | N | 0.0727285 |
| B | 0.015561 | O | 0.0644209 |
| C | 0.0413852 | P | 0.0228467 |
| D | 0.0355562 | Q | 0.000794285 |
| E | 0.129048 | R | 0.0737015 |
| F | 0.0228184 | S | 0.0726779 |
| G | 0.0152493 | T | 0.0940115 |
| H | 0.0378366 | U | 0.0327715 |
| I | 0.0714692 | V | 0.0109555 |
| J | 0.00103988 | W | 0.017412 |
| K | 0.00637232 | X | 0.00448079 |
| L | 0.0453804 | Y | 0.0149802 |
| M | 0.0244326 | Z | 0.0010467 |
需要说明的是,这张表格并不唯一。不同领域的话术有所区别,其所使用的高频单词也不尽相同,又及各人也会有专属自己的文字习惯,所以频率统计表应该针对不同的场景做选择性的文本统计,以期望求得最准确的字母频率。
现在知道了频率分布情况和密钥长度,接下来就着手求解每一个子密钥了。根据\(c_i = m_i + k_{i \mod d} \mod 26\)可以将原密文分成d个密文子序列 $$ m_0, m_{0+d}, \dots, m_{0+nd},$$ $$ m_1, m_{1+d}, \dots, m_{1+nd},$$ $$ \cdot \cdot \cdot $$ $$ m_i, m_{i+d}, \dots, m_{i+nd}。$$ 其中\( i \in \{0, \dots, d-1\} \land i+nd < l\)。然后,针对每一个子序列\(M_i\)进行频率统计,求得在该密文子序列里面每一种字母出现的频率得到表H。如果每一个密文子序列足够的长,可以认为表H里面的频率分布应当对应加密前的明文字母分布,例如在表H里面出现次数最多的字母所对应的明文是E。那么这个过程仅仅只是对比查表吗?当然不是,起始还可以借助程序自动计算来代替这个过程。怎么做呢? 现在有两张频率分布表P和H,观察它们的直方图,例如表P
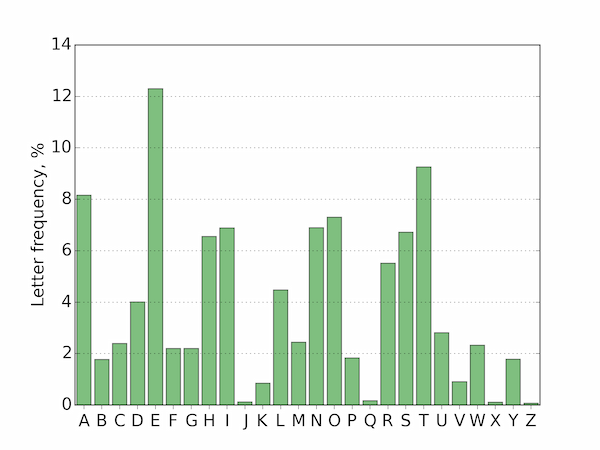
不难理解,表P向右偏移k个距离就是表H,即\( P[i] \approx H[i + k \mod 26] \),k即是当前序列所对应的子密钥。然后计算 $$ C(k) = \sum_{i=0}^{25} (P[i] - H[i + k \mod 26])^2, k \in \{ 0,\dots,25 \},$$ 当C(k)值为最小的时候,也就是说原表P偏移以后和表H的差异最小,可以认为其k就是对应的子密钥。重复对每一个子序列进行表H的统计和C(k)的计算,攻击者将恢复出完整的密钥。 下面是计算子密钥的代码片段
int subkey;
int NUMCHARS = 26;
double min = 65535;
for (size_t k = 0; k < NUMCHARS; k++)
{
C_k = 0.0;
for (size_t i = 0; i < NUMCHARS; i++)
{
C_k = C_k + (P[i] - H[(i+k)%NUMCHARS])*(P[i] - H[(i+k)%NUMCHARS]);
}
if (C_k < min)
{
min = C_k;
subkey = k;
}
}