梅克尔树被发明的初衷,是为了给大量的数据做一个简短的声明,即使数据被拆成若干个部分保存,也能通过梅克尔树来判断最后组合起来的整体的正确性。因为如果某一部分数据被修改或者遭受损坏,最后就无法得到与之前相同的根哈希。
不难理解,能够这么做的前提是已知所有的数据,才能使用梅克尔树。但在区块链领域,每一种链一直都在产生新的区块。2012年,比特币核心开发者Peter Todd遇到了类似的问题。在为一堆不停增长的数据求根哈希的时候,他需要找到一种办法来方便快捷地向梅克尔树上新增叶子节点,同时保证求取根的过程尽量简单,于是他发明了梅克尔山脉(Merkle Mountain Ranges, )——一种专为不停增长的数据整体求根哈希的结构。本文将详细介绍梅克尔山脉及其应用。
梅克尔山脉的必要性
为了解释梅克尔山脉的必要性,我们需要回顾一下梅克尔树的弊端。梅克尔树使用的前提是已知所有的数据。同样的,为了声明一个区块之内的所有交易,也必须提前已知所有待声明的交易。SPV节点在获得区块头以后,便得知了关于此区块之内所有被记录的交易的声明,即梅克尔树根。
此时,即使SPV节点向不同的全节点去质询此区块记录的不同的交易,它依然有信心断定,自己依照证据所得出的结论同样有效。通过梅克尔树根,既能维持对交易记录完整性的承诺,又能保护SPV节点免受对单一全节点的依赖性,从而避免单一故障点风险。
梅克尔树根能够对“静态数据”提供完整性承诺,“静态”意味数据不增不减不变。举个例子,一部电影成品就可以看作是静态数据。当用户通过P2P网络下载一部电影时,首先向一个可信节点获取该电影文件的梅克尔树根,然后从其它陌生节点下载该电影不同的片段并在本地完成组合,只要计算组合文件的梅克尔树根依旧和信任节点提供的树根相同,那么即可确认该组合文件是完整且正确的。
但在区块链领域,“静态数据”并不常见,每一种链都在一直产生新的区块,即待声明的数据会不停地增加新的内容。此时,SPV节点为了缓解存储要求,选择只同步区块链的头,通过梅克尔树根去验证区块内交易的正确性。
随着行业的蓬勃发展,应用于不同场景的区块链项目日益增多。为了支持不同区块链之间的跨链交易,需要保存越来越多的不同的区块链的头部数据,验证节点所面临的存储压力会越来越大。
于是,斯坦福大学的博士生Benedikt等人在一篇发表于国际密码研究学会(IACR,密码学领域的顶级协会)的论文[^1]中提出了一种新型的区块头结构,其中一个字段用来保存梅克尔山脉的根哈希,通过某区块的MMR根哈希就能对此区块之前所有的区块信息做一次声明。这样,验证节点最终需要保存某区块链的最新区块即可,几乎可以说是颠覆了之前SPV节点所面临的困境。
下面来介绍一下基于梅克尔树的变体 —— 梅克尔山脉。

梅克尔山脉是什么?
Peter Todd的思路[^2]是这样的:既然有时候会出现凑不齐一棵满二叉树的情况,那干脆就拆成几个高度较低的满二叉树(也就是山),然后再通过山峰求取最后的根。而生成父节点的规则是这样的:当同一高度出现左右个兄弟节点,即合并生成一个父节点。而高度为0的最底层节点,即代表新增的数据。一个叶子数量为7的MMR结构如下所示
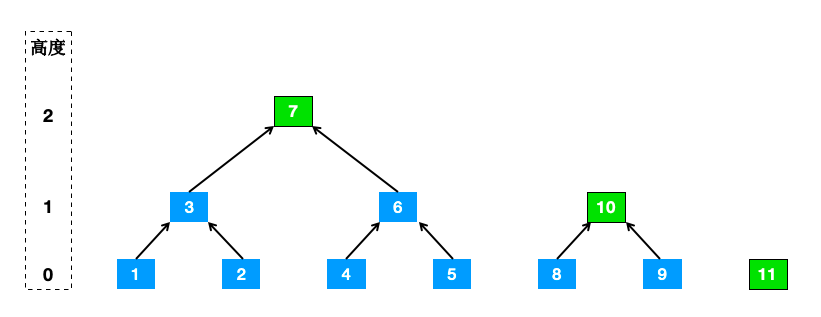
从1开始,按照生成的顺序对节点进行编号。我们把每个满二叉树称作一座山,山顶的节点叫做山峰。最后按照从最低山峰向最高山峰的顺序,计算MMR的根哈希。在上例中,设最低峰为P11、次低峰为P10、最高峰为P7,则根哈希如下
root = Hash(Hash(P11 + P10) + P7)
当再来一个节点(编号为12),则叶子数量为8的MMR结构如下所示
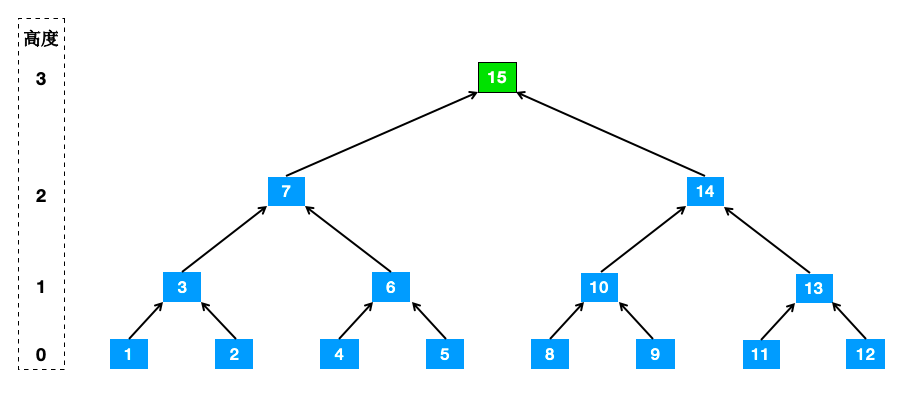
此时根哈希即为最高峰P15。
root = P15
如果想要为某叶子节点构造证明其存在于MMR中的证据,规则也十分简单:
- 构造子树从叶子节点到山峰的 merkle proof
- 拱起右侧山峰,计算其mmr root,结果加入proof
- 将左侧山峰依照自右向左的顺序加入proof
只要验证节点最后依照证据能够计算获得相同的MMR根,即证明通过。
梅克尔山脉的应用
梅克尔山脉结构可以随着叶子数量的增长而动态变化,天然地适应了区块链不断出块的特点。假设以最新区块之前的所有区块作为叶子节点,其构成的MMR结构的根哈希保存在最新区块的头部。这意味着,每一个区块其实隐藏了之前所有区块的信息,即使不保存所有区块的头部,验证节点也能根据MMR根哈希判断最新区块是否有效。
假设当验证节点收到最新区块,为了证明该区块确实属于诚实最长链的最新区块,验证节点会继续向证明节点质询之前若干个区块(即叶子)的信息,证明节点必须提供关于被质询区块的MMR证据,用来证明该区块确实与最新区块同属于一条链。因为MMR根哈希承诺了之前所有的区块,恶意节点无法产生属于诚实分叉上区块的MMR证据,也不能通过提前准备好诚实最长链上的区块来欺骗验证节点。
只有当所有被质询的区块都能提供正确的MMR证据,加以被质询区块的有效性(例如正确的PoW)得到验证,验证节点才会选择相信它所收到的最新区块确实属于诚实最长链上的最新区块。
Benedikt在他的论文里面提供了一种采样算法,如果存在恶意节点造假,该采样算法能够以极高的概率命中无效区块,从而断定收到的最新区块不属于诚实的最长链。
将MMR结构应用在区块链上,需要修改区块头部的数据结构,这相当于一次硬分叉。鉴于比特币网络的自治情况,要想达成这样的共识,难度不小。目前来看,尽管MMR短期内获得社区一致认可与支持的可能性尚且不高,但由于区块链行业将面对的越来越多的跨链交易,终有一天对于方便高效的区块信息验证的需求会引起人们对于MMR的兴趣。