在前一篇文章里,笔者介绍了如何使用梅克尔树给一个区块里的所有交易生成一个哈希,作为树根存储在区块头,以及解释了当交易数量不足时,为什么需要引入的冗余信息来「凑齐」一棵完整二叉树,最后说明了比特币网络如何避免由于冗余信息所引起的潜在双花攻击。
在前文里,笔者还没有谈到的事情是如何判断一笔交易确实存在于某个区块之内?这就是本文想要解释的内容。
可以简单地理解,梅克尔树根相当于一种声明,声明了一个区块包含的所有交易。那么节点凭什么相信该声明就是有效的呢?
现在某SPV节点想要确认一条交易记录是不是有效的,也就是该交易是不是包含在区块链上的某个区块里面。它需要向全节点发送一次问询,告知其交易所在的区块ID,然后全节点会在区块链上找到此区块,并且从其中的梅克尔树上提取一条证据返回,该证据又称梅克尔路径(Merkle Path)。所谓梅克尔路径指的是,从某叶子节点出发,往上溯源直到根节点,这条枝干即称作梅克尔路径。
SPV(Simplified Payment Verification)节点:仅仅保存所有区块的头部,并不保存区块里的交易记录,无法独立判断交易的有效性
全节点(Full Node):保存完整区块链的节点,可以独立验证每一笔交易。
通常把发送询问的节点称作验证节点,把提供证据的节点称作证明节点。凭借梅克尔路径,验证节点就可以判断它询问的交易究竟是不是记录在该区块里。
现在,证明交易的有效性就等价于,此路径确实存在该区块的梅克尔树中。怎么证明呢?
给
你
一
柱
香
的
时
间
诸位读者还记得梅克尔树中每个节点代表什么嘛?每个节点的标签都是一串哈希值,其中叶子节点的标签是交易的哈希,兄弟节点的哈希串联之后经哈希函数计算得到父节点的哈希。
现在,验证节点已经知道的信息有:某条交易,交易所在的区块头(区块ID,梅克尔树根),交易在此区块里的编号。从交易内容可以计算对应的叶子节点哈希,从区块头可以获得区块ID和梅克尔树根,证明人根据交易编号在区块内提取证据。
因此,只要证明节点返回的证据能够令验证节点相信,存在一条从该交易的叶子节点到梅克尔树根的路径,即证明通过,也就是该证据能够帮助验证人由叶子节点哈希推导出根节点哈希。
从叶子节点开始往上计算父节点的哈希,额外需要的信息是其兄弟节点。只要补全路径上每一个节点的兄弟节点,验证节点就能不停地计算,直到获得根节点的哈希。
最后验证节点将计算出来的根节点,与已知的区块头中的梅克尔树根比较,如相等则证明交易存在于区块中,否则不存在。
我们再以一个小小例子来说明以上过程,请看下图
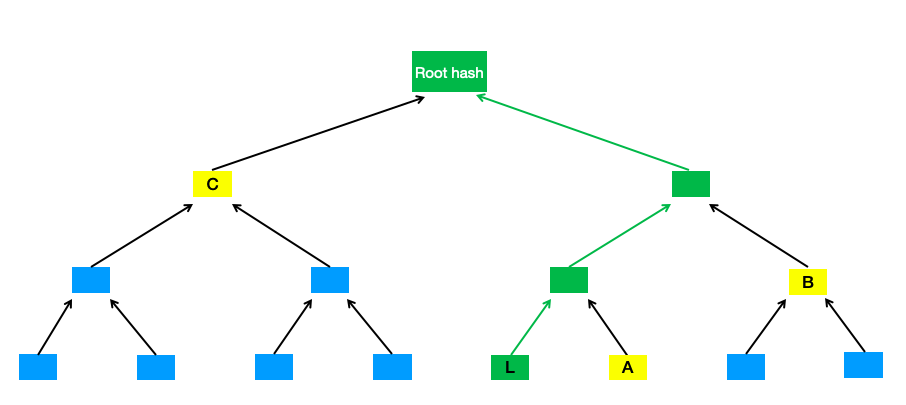
在某区块的梅克尔树中,包含了8条交易的记录。假设验证节点想要知道该区块中编号为L的交易记录是否真实,证明节点收到请求以后,从梅克尔树中找到从编号为L的叶子节点到根节点的路径,即上图中绿色线条。接着安装从下往上的顺序,将路径上所有节点的兄弟节点依次加入证据里。如图中黄色节点所构成的队列A,B,C,这就是证据的内容。
此过程在中本聪最初实现的代码里面如下所示,函数GetMerkleBranch返回的vMerkleBranch即证据
vector<uint256> GetMerkleBranch(int nIndex) const // zero based index
{
if (vMerkleTree.empty())
BuildMerkleTree();
vector<uint256> vMerkleBranch;
int j = 0;
for (int nSize = vtx.size(); nSize > 1; nSize = (nSize + 1) / 2)
{
int i = min(nIndex^1, nSize-1); // nIndex^1 = nIndex+1 or nIndex-1
vMerkleBranch.push_back(vMerkleTree[j+i]);
nIndex >>= 1; // to the parent node
j += nSize;
}
return vMerkleBranch;
}
当验证节点收到证据以后,事情就简单了。它需要做的就是,从证据队列里面取出第一个元素,即待验证叶子节点的兄弟节点,按照左节点在前,右节点在后的顺序串联起来,然后经过哈希函数计算,得到父节点哈希。然后将父节点与队列里的下一个元素做同样的处理,重复以上过程直到队列为空。
此刻,验证节点获得了一个最终的哈希,即「根节点」。如果该交易确实存在于区块当中,那么凭借证据经过计算获得的根哈希应该等于验证人已知的区块头部的梅克尔树根。
实现验证过程的代码如下
static uint256 CheckMerkleBranch(uint256 hash, const vector<uint256>& vMerkleBranch, int nIndex)
{
if (nIndex == -1)
return 0;
foreach(const uint256& otherside, vMerkleBranch) // otherside is a element in vMerkleBranch
{
if (nIndex & 1)
hash = Hash(BEGIN(otherside), END(otherside), BEGIN(hash), END(hash));
else
hash = Hash(BEGIN(hash), END(hash), BEGIN(otherside), END(otherside));
nIndex >>= 1; // forward through the path to merkle root
}
return hash;
}
当返回的hash等于区块头部的梅克尔树根,即验证通过。在我们的例子里,则有以下表达式结果为真
merkel_root == Hash(C + Hash(Hash(tx + A) + B))
现在来说明一下,为什么使用梅克尔树作为验证数据的手段是高效的。
假设一个区块记录的交易数量为$2^N$ ,其路径长度恰好等于$N$。也就是说,当交易数量指数增长时,梅克尔路径的节点数量仅线性增长,其速率要远远慢于交易的增长速率。观察下表也可以得到
| 交易数量 | 区块近似大小 | 路径哈希数量 | 路径大小 = 32 x 哈希数量 |
|---|---|---|---|
| 16 | 4KB | 4 | 128 Bytes |
| 512 | 128KB | 9 | 288 Bytes |
| 2048 | 512KB | 11 | 352 Bytes |
| 65535 | 16MB | 16 | 512 Bytes |
当交易数量从16增长到65535时,区块存储空间从4KB增加到16MB,而梅克尔路径长度仅从4增长到16,证据大小仅从128字节增加到512字节。
有了梅克尔树和全节点,SPV节点并不需要保存大量的交易记录,就能方便得验证某条交易的有效性。当然这样的节点也就丧失了独立性,必须依赖其它节点才能正常工作。
至此,笔者已经介绍完了什么是梅克尔树,怎样计算树根,以及如何为一笔交易构造证据,和节点如何检查证据的有效性。现在留一个小小问题给诸位读者,检查一下是否准确掌握梅克尔树的用法。
某区块一共包含5笔交易,找出最后一笔交易的梅克尔路径。
另外,困于不能方便地增添新的叶子节点进入已有的梅克尔树,Peter Todd在2012年发明了另外一种变体—梅克尔山脉(Merkle Mountain Ranges),解决了当需要不停新增叶子节点的情况下,如何快速计算根节点。
接下来,笔者将详细介绍梅克尔山脉的基本原理和它想要解决的问题。