在不久之前,密码学还不能被称作一门学科,顶多是一种手艺。在古典密码学时代,密码系统的安全仅仅取决于设计者和攻击者的创造力和技巧,人们并不能证明一种密码系统的安全性究竟几何?也没有对密码系统的诸多元件有清晰而明确的定义。
密码学真正成为一门系统而逻辑严密的学科,源自二战时,交战双方终于意识到通信的安全性对于战局的决定性影响力。德国佬的Enigma机器曾使盟军头痛不已,直到图灵和波兰数学家的合作才终于破译德军的军事情报信息。由战争带来的对于安全通信的需求,在战后的冷战时代未曾消减,密码学的理论研究终于大放异彩。今天,几乎所有关于密码理论的基本概念都源自那个令人不安的时代。
本篇小文将介绍现代密码系统的几种安全模型,及其相互关系。
三种攻击类型
俏皮的密码学家们,把密码系统的设计与破解想象成一场智力的游戏。在这个游戏场景中,密码系统的设计者被称作挑战者,他将带着自己设计的密码机制去挑战系统的破坏者,也即攻击者。无论是攻击者还是挑战者胜利,都会使密码系统的设计越来越完善和安全。这是一场没有结束的竞赛。
密码学家定义了三种不同的攻击类型,它们是
- CPA(Chosen-Plaintext Attacks):选择明文攻击,在这个攻击模型里面,攻击者拥有一个
Oracle,它只能用来加密攻击者提交的明文,并返回结果; - CCA1(Chosen-Ciphertext Attacks):1型选择密文攻击,此时攻击拥有一个即能加密也能解密的
Oracle,并返回结果给攻击者,但是攻击者只能【一次性提交所有】的明文或者密文给Oracle处理; - CCA2(adaptive Chosen-Ciphertext Attacks):2型选择密文攻击,攻击者拥有如1型相同能力的
Oracle,不同的是攻击者可以【逐次提交】想要加密或者解密的内容,然后根据返回的结果,构造下一个明文或者密文并提交给Oracle。
以上描述的三种攻击类型,区分了现实中攻击者所能支配的资源。例如,二战中英军曾获取到了德国人的Enigma机器,却不知道密钥,他们只能使用机器去加密输入的内容,然后观察结果以期望求得密钥簿,所谓选择明文攻击(CPA)。
三种安全目标
其实所谓“安全”的定义并没有一个严格又明晰的说法,但是密码学家还是尽可能给出了一些具有确定标准的安全概念。通过理论研究,密码学家为一个密码系统描述了三种安全目标:
- IND(Indistinguishablity):不可区分性。攻击者发送两个明文
m0, m1给挑战者,经过加密以后返回一个密文c。如果攻击者无法判断密文c是属于m0还是m1,即攻击者判断正确的概率小于等于0.5,则挑战者胜。称挑战者设计的密码系统具有不可区分的性质IND;
A C
| m0,m1 |
| --------------> |
| c |c=Enc(k,mb)
| <-------------- |
| b' |
| --------------> |b=b' ?
- RoR(Real or Random):不可辨别随机性。攻击者从明文空间
S里选择一条明文m,并将二者发送给挑战者。挑战者随机在S中再抽选一条明文x,决定加密m或者x,将加密结果c返回给攻击者。如果攻击者无法判断挑战者加密的是m还是x,则挑战者胜利。称该密码系统具有不可辨别随机型;
A C
| m,S |
| --------------> |
| c |c=Enc(k,m) if b=0
| <-------------- |c=Enc(k,x) if b=1 x <== S
| b' |
| --------------> |b=b' ?
- NM(Non-Malleability):不可延展性。攻击者直接将明文空间
S告知挑战者,挑战者从中选择两条明文x0,x1,加密x0并将结果y返回给攻击者。攻击者修改y为y',定义一种二元关系R,例如不相等,挑战者对y'进行解密计算得到结果x'。如果x0与x‘满足关系R的概率小于获等于x1与x‘满足关系R的概率,例如P(x0 != x') < P(x1 != x'),则挑战者胜利。称该系统具有不可延展性。
A C
| S |
| --------------> |
| y |x0,x1 <== S
| <-------------- |y=Enc(k,x0)
| R, y' |
y'!=y| --------------> |x'=Dec(k,y') ==> P(R(x0,x')) > P(R(x1,x')) ?
它们的谱系
现在有了三种类型的攻击者,以及密码学家所追求的三个安全目标。于是,有了如下的关系
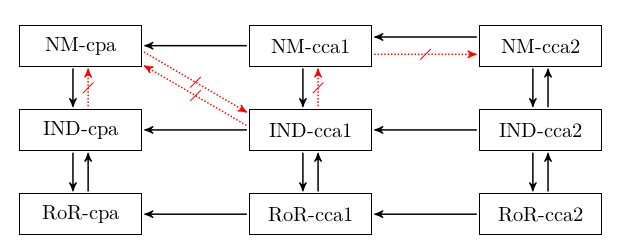
以上各种关系可以通过演绎法证明得出,笔者会在另外一篇文章里详细解析解释证明过程。