在前一篇文章,我们详细解释了基于不变难度的超轻节点如何验证区块的有效性以及其验证结果正确概率的模型。这个模型的前提是基于理想状态设定的,能够帮助读者更容易理解超轻节点的工作流程和其背后的数学原理,但在真实的区块链行业,基于PoW的共识算法会随着参与网络竞争的节点数量和运算能力改变而周期性调整难度目标。这意味着,节点必须检查区块的PoW是否满足难度调整函数。
在本篇文章,我们将首先介绍中本聪为比特币网络设置的难度调整函数,然后用更形式化的方法为读者解释难度调整函数,最后说明在可变难度下超轻节点如何检查区块的PoW。
中本聪难度调整机制
整个比特币网络以大约每十分钟生成一个区块的速度稳定且安全地运行了近十年时间,这期间没有任何人的比特币被暴力剥夺或者交易记录被恶意篡改。然而十分钟的出块速率只是一个理想的状态,真实情况是,随着网络环境的改变,比如节点的加入或者离开,挖矿设备的更替等,都会导致出块速率的波动。
为了平衡这种波动,让区块产出的速率尽可能地保持稳定,中本聪引入了难度调整机制:每隔2016个区块,所有节点将独立计算新的难度目标值。在理想的情况下,难度目标和全网哈希算力能够恰好匹配,这样挖出2016个区块花费的时间应该就是20160分钟,也就是两周。但真实时间往往是或高于或低于这个目标,所以需要调整难度以期能够接近理想出块速率。真实时间与目标时间之比称作调整系数。
简单地说:当出块速率低于10分钟,网络将提高挖矿难度(减小难度值);反之,将降低难度(增大难度值)。
调整函数如下
New Target = Old Target * (Actual Time of Last 2016 Blocks / 20160 minutes)
在Bitcoin Core里,难度调整函数的代码如下
// Limit adjustment step
int64_t nActualTimespan = pindexLast->GetBlockTime() - nFirstBlockTime;
if (nActualTimespan < params.nPowTargetTimespan/4)
nActualTimespan = params.nPowTargetTimespan/4;
if (nActualTimespan > params.nPowTargetTimespan*4)
nActualTimespan = params.nPowTargetTimespan*4;
// Retarget
const arith_uint256 bnPowLimit = UintToArith256(params.powLimit);
arith_uint256 bnNew;
bnNew.SetCompact(pindexLast->nBits);
bnNew *= nActualTimespan;
bnNew /= params.nPowTargetTimespan;
为了抵御潜在的攻击,实际的调整系数会被限制在 $[1/4, 4]$ 之间。要理解这么做的原因,我们还需回顾一下区块链的基本结构:在比特币网络,矿工们总是选择从**累计最难(即难度目标总和最小)**的那条最长链末端开始挖取下一个区块。假设不限制调整系数,恶意节点可以强行设置一个难度极高的PoW目标。这样即使恶意节点的算力不足,也有可能因为运气足够好而成功挖出区块,从而短暂地超过诚实节点成为最难最长链,此时区块链就出现了分叉。这种攻击手法称作 Difficulty Raising Attack。
因此为了阻止此类攻击的发生,可以通过限制调整系数,使得难度设定过于离谱的PoW变为无效。但是如此一来,有可能会导致难度调整函数无法准确得到下一轮的难度目标,从而导致出块速率无法通过一次调整就能够稳定在10分钟。可以说,这是为了保障网络安全性而做出的必要的妥协。
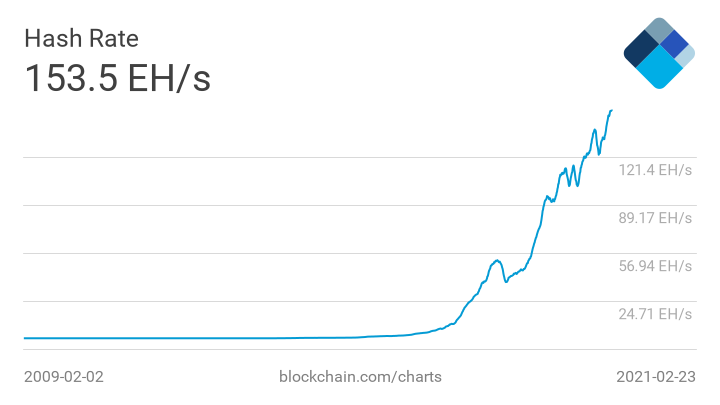
可以看出,上述的PoW难度调整机制是十分简单且有效的,但它最终将比特币引入了算力争霸的赛道。众所周知,比特币挖矿消耗的能量越来越多,其网络一年消耗的电能已经超过阿根廷的年发电总量。随着参与挖矿的节点越来越多,以及挖矿设备的算力越来越强(CPU -> GPU -> ASIC),如今全网算力已达 153.5 EH/s,即每秒可做 $153.5 \times 10^{18}$ 次哈希运算。
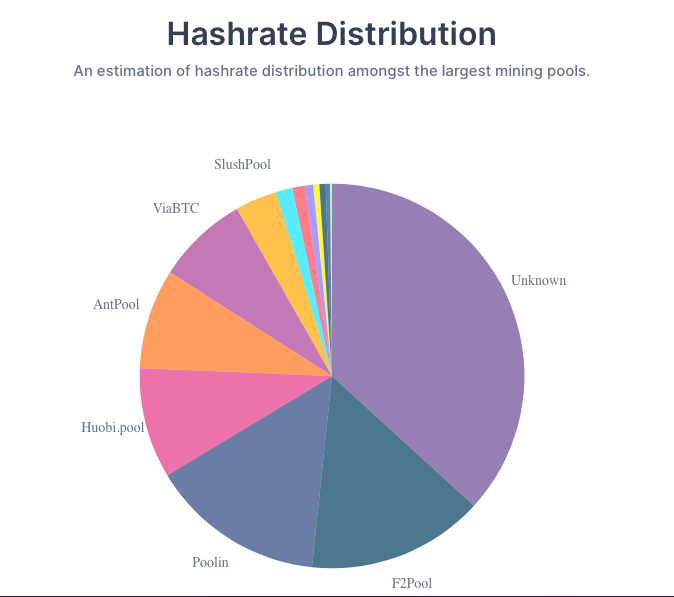
随着矿池的出现和矿机的专业化,挖矿算力越来越集中于几个大矿池,使得普通个人只能通过购买手段来获取比特币。这引起了一些人对于比特币安全性的担心,他们认为今天的局面有悖于当初中本聪设想的去中心化货币。第三方的统计数据显示,几大矿池的算力之和已经超过了全网总算力的50%,因而理论上如果它们达成共谋,针对网络的「51%攻击」就很有可能成为现实。
形式化难度调整
为了读者能够更准确地理解PoW链的难度调整机制,我们将用更专业的数学语言来进行进一步的解释
首先约定几个术语:
目标难度:$T = 2^\lambda$ ,$\lambda$ 为难度参数,可动态变化。$T$ 值越小,则越困难。
一次哈希运算就挖矿成功的概率:$T/2^\kappa = 2^{\lambda - \kappa}$,$\kappa$ 为哈希函数参数,比特币网络里 $\kappa = 256$,$2^\kappa$ 代表所有可能的哈希值
难度调整周期:$m$ 个区块,在比特币网络 $m = 2016$
一轮竞争:单机做$q$ 次哈希运算
假设参与竞争的每个节点算力相同,第 $r$ 轮竞争挖矿的诚实节点数量为 $n_r$,恶意节点数量为 $t_r$,则此轮一共可进行 $(n_r + t_r) \cdot q$ 次哈希运算,期望挖出区块的数量为 $$ (n_r + t_r) \cdot q \cdot \frac{T}{2^\kappa} $$
假设在上一个难度周期,有 $ n = n(T, R)$ 个节点,经过 $R$ 轮竞争共产生了 $m$ 个区块,难度为 $T$,则有 $$ n \cdot q \cdot R \cdot \frac{T}{2^\kappa} = m $$ 在新的难度周期内有$n’$个节点,调整目标:经过 $\Delta$ 轮竞争之后能够产生 $m$ 个区块,即 $$ n’ \cdot q \cdot \Delta \cdot \frac{T’}{2^\kappa} = m $$ 经由两式相比,得到 $$ T’ = \frac{n}{n’} \cdot \frac{R}{\Delta} \cdot T $$ 并且,抑制难度波动 $$ \frac{1}{\tau} \le \frac{T’}{T} \leq \tau $$ 即 $$
$$
$$ T’ = \tau \cdot T \Longleftarrow \frac{ T’}{ T} > \tau $$
可变难度MMR
在正式介绍可变难度下的超轻验证原理之前,我们还需要对MMR结构体做些改动:此前我们定义每个MMR节点仅仅保存哈希值,现在定义新的MMR节点为 [h, w, t, n, D_start, D_next],其中各个字段的含义如下:
h:当前节点的哈希值w:当前节点下所有节点的累计难度t: 当前节点记录的时间戳n:当前节点下子树的尺寸D_start: 当前节点的难度目标D_next:前节点指定的下一个相同高度节点的难度目标
父节点p的定义如下所示,其中l,r分别代表左右子节点
[
h = H(l.h, r.h),
w = l.w + r.w,
t = l.t + r.t,
n = l.n + r.n,
D_start = l.D_start
D_next = r.D_next
]
为了简化分析过程,设置难度调整函数的周期为 $m = 2^n$ 个区块,以及MMR结构的叶子数量也为$2^n$,例如下图
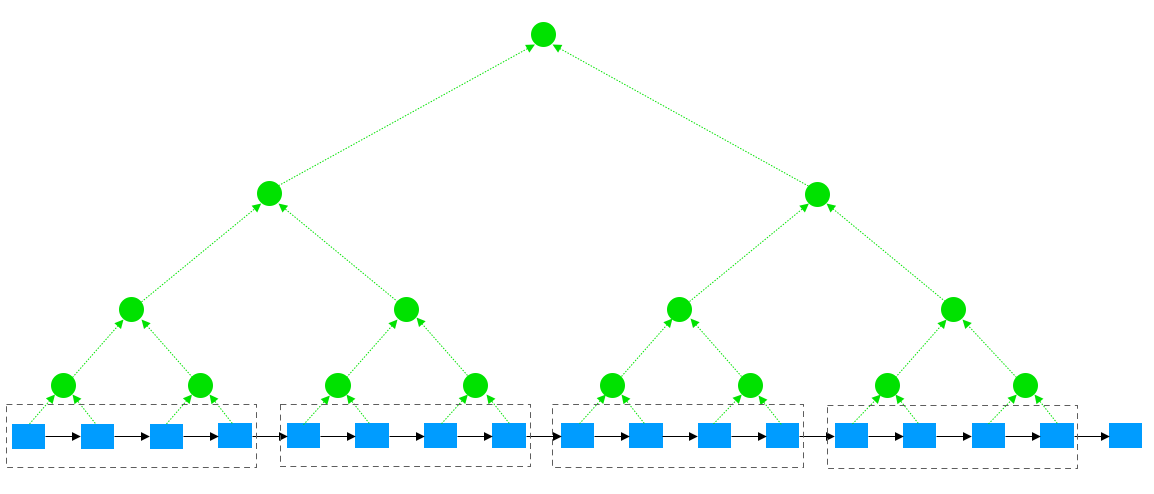
超轻节点如何验证某个被采样区块的MMR证据:
- 由兄弟节点计算得到父节点
- 验证
l.D_next == r.D_start - 对于兄弟节点,其难度目标应具有一致性
- 如果节点高度不大于
log(m),其难度目标应与此周期内兄弟节点的难度目标相同 - 如果节点高度大于
log(m),意味着该节点之下,发生了难度调整,检查此节点的D_next是否符合难度调整函数的计算结果
- 如果节点高度不大于
为了检查难度一致性,超轻节点需要判断【是否存在一组难度调整过程,决定了当前节点的各项参数?】
检查高度不大于log(m)节点的难度一致性较为简单:高度不大于log(m)节点的难度参数w, D_start, D_next完全由此周期决定,即检查
p.w == l.w + r.w
p.D_start == l.D_start
p.D_next == r.D_next
l.D_next == r.D_start
检查高于log(m)节点的难度一致性则更为复杂:由于节点的难度参数受到了难度调整函数的影响,因此需要检查难度调整是否符合要求。我们定义累计难度w为节点之下所有区块的难度总和。经历若干次符合要求的难度调整之后,该节点的累计难度w总是被限制在某个区间范围[w_min, w_max]之内,即存在一组难度调整操作满足D_next = F(D_start, w),F代表若干次难度调整操作。
因此只要计算出当前节点累计难度的区间,然后检验累计难度w是否在此区间,就能判断D_next是否有效。为了简化分析,不妨假设某节点经过n次难度调整,并且满足
$$
\tau^{k} \cdot D_{start} = D_{end}, \ k \leq n
$$
为了达到区间上限,应该以最大幅度对难度值进行若干次的增加
New Target = t * Old Target
然后再以最大幅度进行若干次减少难度值
New Target= 1/t * Old Target
难度调整过程如下图所示
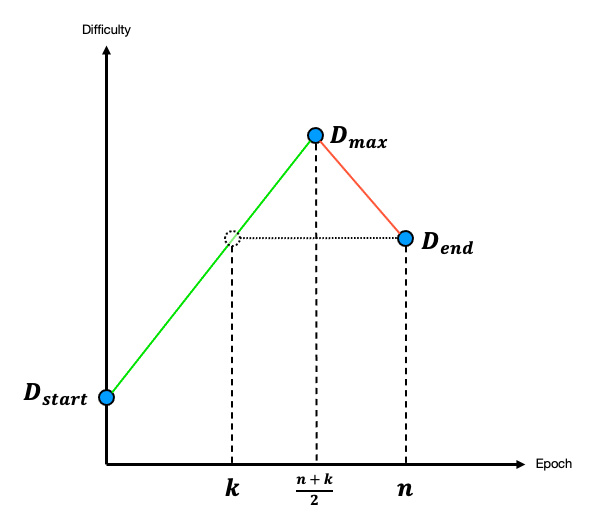
此时的难度调整曲线与座标轴围成的面积即是累计难度的最大值,即
$$ w \leq D_{start} \Big( \Sigma_{i = 0}^{\frac{n+k}{2}} \tau^i + \Sigma_{i=k+1}^{\frac{n+k}{2} -1} \tau^i \Big) = D_{start} \cdot \frac{(\tau + 1) \tau^{\frac{n+k}{2}} - \tau^{k+1} -1}{\tau -1} = w_{max} $$
同理,为了求得区间的下限,应该先以最大幅度对难度值进行若干次的减少,再以最大幅度对难度值进行若干次的增加,如下图所示
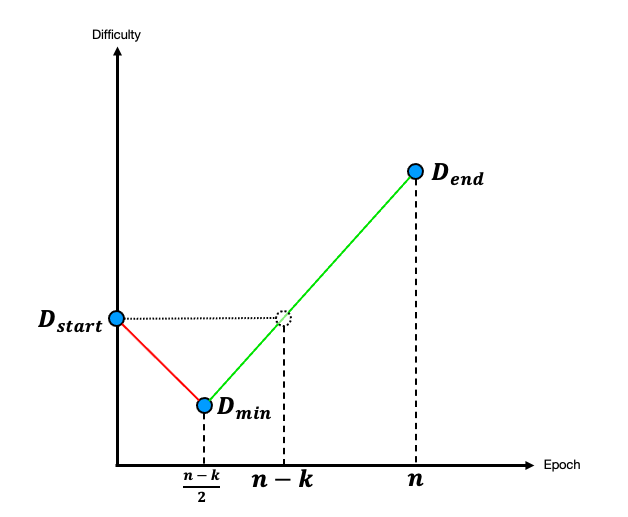
求得最小累计难度为 $$ w \geq D_{start} \Big( \Sigma_{i = 0}^{\frac{n-k}{2}} \tau^{-i} + \Sigma_{i=1}^{\frac{n-k}{2}-1} \tau^{-i} + \Sigma_{i = 0}^{k-1} \tau^{i} \Big) = D_{start} \cdot \frac{\tau^k + \tau - (\tau +1 ) \tau ^{\frac{n+k}{2}}}{\tau -1} = w_{min} $$
现在,我们再来举一个例子说明如何利用累计难度来判断区块PoW的有效性。
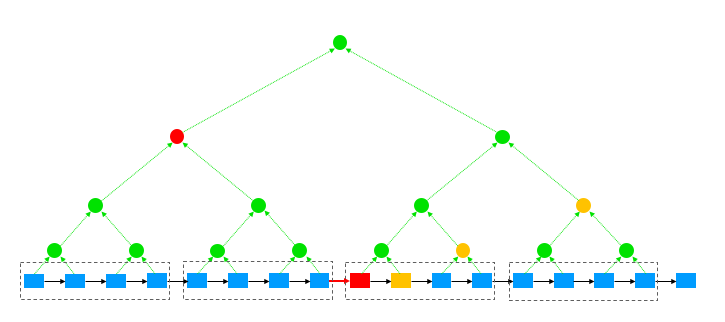
上图中底层蓝色区块代表MMR结构中的叶子节点,父节点由兄弟节点产生。假设图中红色区块被采样,图中黄色图形和左上方红色节点组成该区块的MMR证据。如果红色区块的PoW造假,即其难度目标不符合难度调整函数的结果,也即左上方红色的MMR节点的D_next值无效。
根据该红色节点在MMR结构中的位置,可以得出其下所有区块共经历几次难度调整,即n。再根据此节点的D_start和D_next(即D_end),可以得出k值。
获得D_start, n, k之后,可以求出累计难度的区间,最后再检查红色节点的w是否属于该区间。如果不属于,即判断红色区块的PoW无效。
对于MMR证据里面每一个节点都进行以上检查,本质上就是为了确定最新区块之前的区块的PoW没有造假,而最新区块的PoW有效性由其存储的MMR根节点信息提供证明。
结束语
至此,我们终于完整地解释了MMR在超轻验证中的应用原理,如果读者有不甚清楚的内容或者有所勘误,欢迎留言交流。区块链行业历经十余年的发展,对现实世界的影响日渐深远。其安全性建立在底层坚固的数学模型之上,这也是人们对区块链发展前景充满信心的原因。我们在研究基础理论的同时,也将时刻关注行业的最新动态,期待为读者继续展示本行业迷人的风云变幻。