为了验证交易的合法性,加密货币例如比特币和以太坊,要求节点必须验证区块链的有效性。节点在接入加密货币网络之初,需要花费数小时以及相当大的磁盘空间来下载、验证和存储所有区块。然而一些客户端由于缺乏必要的资源(带宽、存储),无法独立验证交易,必须依赖全节点。比特币和以太坊均提供了一种名为SPV客户端的方法,SPV客户端仅仅验证和保存所有的区块头。然而,仅仅保存区块头的存储要求也是随着链长的增长而线性增长。至2021年1月为止,以太坊网络的SPV客户端需要存储的区块头数据已经逼近 6 GB。对于资源更受限的 IoT 设备,其存储上限可能都无法达到上述要求。
本篇文章将介绍一种新型验证手段(新的区块头结构)来帮助超轻节点判断区块的有效性,甚至不需要保存完整的区块头链,节点也能以极高的概率做出准确判断,每次验证通过之后仅需更新本地唯一保存的最新区块。
在上一篇文章,我们介绍了梅克尔山脉的基本结构和验证方法。在本篇文章,我们将首先设置一个攻击模型,然后介绍基于此模型下MMR的验证过程,最后详细解释采样算法命中无效区块的概率问题。
PoW 挖矿规则
在基于PoW的加密货币网络中,参与竞争的节点朝着所有人都一致认可的**难度目标(T)**进行运算挖矿,直到有节点第一个得到符合要求的结果,如此便产生了一个合法的区块,那个幸运的节点便获得系统奖励的比特币和区块中交易产生的手续费作为报酬,而网络中所有节点便基于此区块继续竞争下一次出块。出块的过程称作挖矿,参与竞争的节点称作矿工。
为了方便后续理解,先正式地介绍一下挖矿过程:
假设高度为 $n$ 的区块头是 $B_n$,难度目标为 $T$,哈希函数为 $H(\cdot)$,则合法区块的必要条件是 $H(B_n) \leq T$。由于哈希值的不可预测性,矿工们只能不停修改区块头的
Nonce字段,直到 $H(B_n) \leq T$,挖矿成功。
$T$ 值越大,意味着满足条件的哈希值 $H(B)$ 越多,即一次哈希运算得到 $H(B) \leq T$ 概率越大 ,也就越容易出块。所以, $T$ 值与难度成反比。
网络中的诚实节点会遵循公认的难度目标进行挖矿,但是有些节点为了某种目的,故意设置更容易的难度目标(即更大的 $T$ 值)。这样,恶意节点能够以较低的算力作为代价,加快出块速度。但是这些区块是无效的,因为其 PoW 结果不为其它节点所承认。于是,区块链出现了分叉
攻击模型
在一个加密货币网络里面,参与竞争的各方节点通过一致的 PoW 挖矿规则,共同维护着网络的安全,中本聪也设计了比特币的奖励机制诱导节点去遵守共识规则来最大化收益。所以,我们可以假设网络中恶意节点的哈希算力要始终小于诚实节点所掌握的算力,令二者之比为 $ c \in [0,1) $。
自分叉之后,诚实节点挖出的区块数量为 $L$,而恶意节点由于算力不足,能挖取的有效区块数量只有 $c \cdot L$。恶意节点为了令某轻节点相信它的区块所在的链是最长链,必须在分叉之后伪造区块(非法的难度值),其数量不少于 $(1-c) \cdot L$。这样,恶意节点的分叉链至少看起来和诚实链一样长。
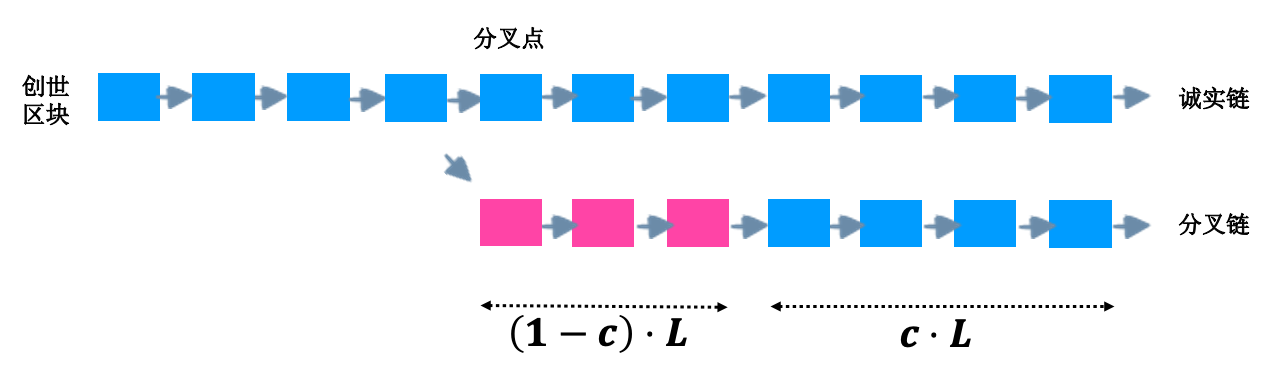
聪明的读者可能会问:为什么无效区块全都集中在靠近分叉点一侧?请继续阅读下文。
在此模型下,轻节点仅仅保存上一次验证通过的最新区块。当其收到一个更新的区块时,需要通过MMR+采样算法来断定其是否属于诚实链:轻节点首先检查新收到区块的PoW有效性,然后按照采样算法向对方质询此区块之前的若干个区块,证明节点需要提供证据来令轻节点相信:被采样的区块和最新区块在同一条链上,并且均满足合法的PoW。只要所有被采样的区块都拥有一个验证通过的MMR证据以及合法的PoW,轻节点就选择新收到的区块作为最新区块,并更新本地的记录。
MMR检查
正如上一篇文章提到,通过在区块头引入新的字段mmr root,每一个区块实际上都是对其之前所有区块的承诺。我们约定如下的符号:
$n$:区块链的最新高度
$B_i$:高度为 $i$ 的区块
$M_i$:前 $i-1$ 个区块组成的MMR结构的根哈希,存储在 $B_i$
$P_i$:$B_i$ 的MMR证据
然后再定义三个函数:
$Get_Proof(M_n, n, i) \rightarrow P_i$:获取区块 $B_n$ 承诺的关于区块 $B_i$ 的证据 $P_i$
$ Get_Root(P_i, n, i) \rightarrow M_i$:根据 $P_i$ 计算前 $i-1$ 个区块MMR根哈希 $M_i$
$Vfy_Proof(M_n,P_i,B_i) \rightarrow 0 / 1$:通过区块 $B_i$ 和证据 $P_i$ 来计算根哈希,如结果等于 $M_n$,则验证通过
验证过程如下
- 超轻节点收到最新区块 $B_n$,获得根哈希$M_n$
- 超轻节点检查$B_n$的PoW是否有效,在不变难度的PoW链上,仅需判断 $H(B_n) \leq T$是否成立;可变难度将在下一篇文章详解
- 如果PoW验证通过,则超轻节点继续向证明节点质询之前某个区块 $B_i$
- 证明节点调用$Get_Proof(M_n, n, i)$返回证据 $P_i$ 和 区块$B_i$
- 超轻节点调用 $Vfy_Proof(M_n,P_i,B_i)$ 检查证据$P_i$,并检查区块$B_i$的PoW
- 超轻节点调用 $Get_Root(P_i, n, i)$ 得到$M_i$,结果再与区块 $B_i$ 中存储的根哈希比较,若相等,则区块 $B_i$ 通过验证
- 超轻节点继续向证明节点质询其它若干个区块,只要存在一个区块验证失败,则拒绝最新区块
为了令超轻节点接受最新区块,需要提供之前若干个区块的证据和有效的PoW来向其证明,最新区块所在的链上没有区块造假。在SPV节点模型中,节点保存了完整的区块头链,能够独立验证链上所有区块的PoW是否有效。而超轻节点仅仅保存上次验证通过的区块,当收到一个新区块的时候,甚至不知道它们是否位于同一条链上。因此,需要新区块所在链上的若干个有效区块来辅助证明其有效性。
如前所述,这是一种基于概率的共识策略。我们将在下一节详细解释采样算法和其概率期望。
采样算法
正是因为最新区块能否被认可取决于被采样的若干个区块的有效性,采样算法对于保障超轻节点做出正确判断至关重要。采样的目的是为了命中无效区块,而无效区块只会出现在分叉点之后,尽可能采样分叉点之后的区块显然能大大提高成功发现无效区块的概率。
我们将采样过程分成若干轮,每轮均随机质询 $k$ 个区块。在第 $ j \in [0, \log{n})$ 轮,采样的高度范围是 $[(1- \frac{1}{2^j})n, n)$,区间长度是 $s_j = \frac{n}{2^j}$。可以发现最初一轮采样范围是完整的区块链,而下一轮采样范围是上一轮的后一半。
由于超轻节点并不知道分叉点的高度,所以一开始需要从整条链上采集 $k$ 个区块。如果运气足够好的话,其中就有无效区块,采样结束,超轻节点拒绝最新区块;否则,进入下一轮继续采样。直到某一轮区间长度 $s_j \leq k$,此时区间内所有区块均被采样。
只有当每一轮的所有被采样区块均有效,才接受最新区块有效。
现在,再来说明一下此策略下的命中概率问题。

假设分叉点的区块高度为 $a$,必然存在某一轮采样 $j$ 满足 $$ (1-\frac{1}{2^j})\cdot n < a \leq (1-\frac{1}{2^{j+1}})\cdot n $$ 即分叉点在第 $j$ 轮采样范围内,却不在第 $j+1$ 轮。则有, $s_{j} / 2 \leq L < s_{j}$。
于是,在第 $j$ 轮,采样区间内无效区块的数量满足 $$ h_j = (1-c)\cdot L \geq (1-c)\cdot \frac{s_j}{2} $$
$k$ 次采样均未能命中无效区块的概率是 $$ P_j = \Bigg(\frac{s_j - (1-c) \cdot L}{s_j}\Bigg)^k \leq \Bigg(\frac{s_j - (1-c) \cdot \frac{s_j}{2}}{s_j}\Bigg)^k \leq \bigg( \frac{1+c}{2} \bigg)^k $$ 超轻节点最终未能命中无效区块的概率为 $$ P(failed) = \prod_{j = 0}^{logn} P_j $$ 又因为 $P_j \leq 1$,所以有 $$ P(failed) \leq \bigg( \frac{1+c}{2} \bigg)^k $$ 最终,成功命中的概率至少为 $$ P \geq 1 - \bigg( \frac{1+c}{2} \bigg)^k $$
随着 $k$ 逐渐增大,超轻节点失败的概率呈指数级降低。如果 $L \leq k$,验证节点将在某一轮命中所有的无效区块,此时失败的概率为〇。
更优的采样算法
在上述算法下,越靠近最新区块,被采样的概率越高,即采样概率随块高梯度增加。此时出现了一组矛盾:虽然总体看来越靠近区块链末端,被采样的概率越高;但在一轮采样之中,区间内所有区块被采样的概率相同。这样的概率分布并非平滑曲线,我们的目标是找到一个平滑且增长的概率密度函数PDF。
在新的策略下,使用 $q$ 次独立重复采样算法:即遵循平滑增长的PDF对区块链进行 $q$ 次采样。
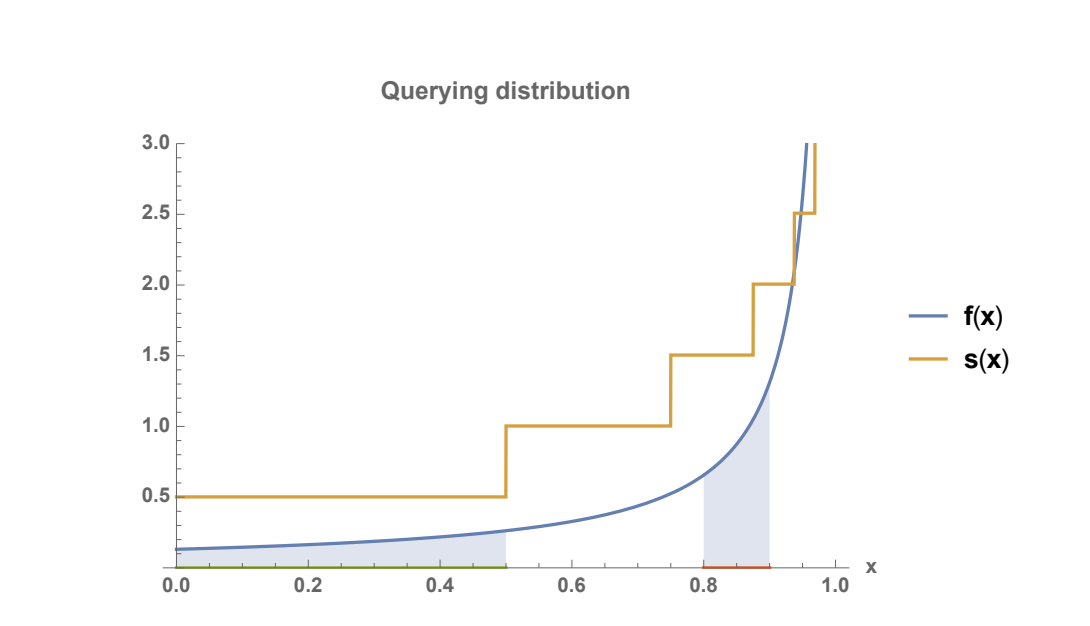
由上图可以解释之前的一个小问题:为什么无效区块总是集中在分叉点一侧?因为这样能减少被命中的概率。
该如何找到这条曲线 $f(x)$ 呢?首先设置:创世区块编号为 0,分叉点区块编号为 $a$,最新区块编号为 1。
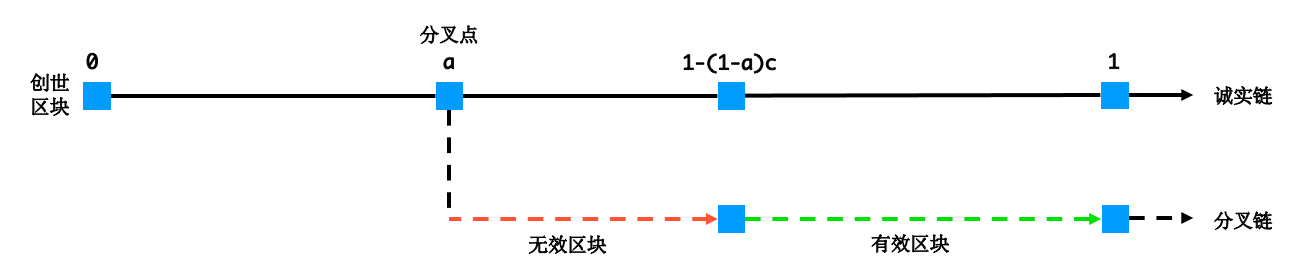
恶意节点挖出的有效区块数量为 $(1-a) \cdot c$,无效区块的编号范围是 $[a, b]\ b = 1-(1-a)\cdot c$。在一次采样过程中,命中无效区块的概率为 $$ p = \frac{\int_a^{b} f(x)dx}{\int_0^1 f(x)dx} $$ 注:分母为归一化系数
考虑到恶意节点可以任意选择分叉位置,一次采样命中的最小概率为 $$ p = \underset{0 \leq a < 1}{min} \frac{\int_a^{b}f(x)}{\int_0^1 f(x)dx} $$ 另外,我们希望,无论分叉点在哪,一次采样命中的概率总能相等,即使分叉点是创世区块,即 $a = 0$ $$ \int_0^{1-c} f(x)dx = \int_a^{b}f(x)dx $$ 上式由差分分析可以解出 $$ f(x) = \frac{1-c}{c(1-x)} $$ 但是, 发现归一化系数 $\int_{0}^{1}f(x)dx = \infty$,不满足PDF定义。于是,超轻节点选择一定会采样靠末端的部分区块,长度占比为 $\delta$,迫使恶意节点不能在此处造假,即 $$ 1-(1-a) \cdot c \leq 1- \delta \Longrightarrow a \leq 1 - \frac{\delta}{c} $$
在区块链末端 $\delta$ 区域,算法命中无效区块的概率为〇。
在可变难度模型下, $\delta$ 区域也能用来计算最新区块的难度目标是否正确,以此判断其PoW的有效性。
于是,新的概率密度函数为 $$ g(x) = \frac{f(x)}{\int_0^{1-\delta}f(x)dx} = \frac{1}{(x-1)\ln{\delta}} $$ 一次采样命中概率无效区块的概率为 $$ p = \underset{0 \leq a \leq 1 - \frac{\delta}{c}}{min} \int_a^{b} g(x)dx = \int_0^{1-c} g(x) dx = \log_{\delta}{c} $$ $q$ 次独立重复采样之后,至少命中一个无效区块的概率为 $$ P = 1 - (1-\log_{\delta}{c})^q $$ 在此概率模型下,超轻节点做出正确判断依赖于三个参数:恶意节点的算力大小 $c$,必采样的区域长度 $\delta$,和随机采样次数 $q$。这是一个依赖真实应用场景的问题,没有统一标准。本文给出一个可能的设置方法:
- 根据对准确性的要求选定一个概率目标 $P$
- 由于无法判断节点是否恶意,可将全网掌握最大算力的单一实体视作可能的作恶者,得到 $c$
- 根据难度调整周期选定 $\delta$ ,其长度应不超过难度调整周期
- 根据以上反推出采样次数 $q$
总结
至此,我们已经详细介绍了如何使用MMR和随机采样算法来帮助超轻节点以极高的概率正确验证区块。以上所有证明均基于不变难度的区块链,其PoW有效性的验证非常容易,仅需判断 $H(B) \leq T$ 是否成立即可。而在实际应用中,例如比特币,挖矿的难度随着竞争环境的改变而周期性调整,因此超轻节点需要额外的信息来辅助检查PoW。我们将在下一篇文章里详细说明PoW难度调整模型,并介绍在可变难度下,超轻节点如何验证区块的PoW。
自2009年至今,比特币网络“无中生有”地创造了超过万亿美元的资产,整个加密货币领域的总市值超过了1.5万亿美元,加密货币正越来越受到市场和机构投资者的关注。在加密货币网络里,全节点以自身的算力和存储空间为代价,始终能够独立验证区块,同时通过挖矿维护着网络的健壮性。这些由不同组织或者个人掌控但遵守共识规则的全节点,也是加密货币网络去中心化的关键所在。
然而,普通用户仅需要在交易的时候验证区块,并没有保存完整区块链的动机。在行业早期,区块链还不够长的时候,SPV节点能够很好地解决这个问题。然而至今天为止,仅以太坊的区块高度已经超过一千万,超轻验证节点因消耗极少的存储资源而具有潜在的实用性。