线性分析 FEAL4

FEAL4(Fast data Encryption Algorithm)由日本密码学家清水明宏和宫口庄司于1987年在日本电信电话株式会社(NTT)任职期间提出，作为一个针对DES的替代加密方案。相比较DES被设计成硬件电路的思路，FEAL4可由纯软件实现，得益于较少的加密轮数(4轮)，其执行速度相当快。本文首先介绍FEAL4以及DES所使用的Feistel加密结构，根据FEAL4所使用的F函数，分析F输入及输出之间的线性关系。然后解释，如何利用该线性关系配合较少的明文密文对，攻击者可以快速破解密钥。

Feistel Network

一切还需要从DES(Data Encryption Standard)讲起。二十世纪七〇年代，蓝色巨人IBM在NSA(后来被Snowden暴光棱镜计划的大名鼎鼎国安局)的资助下，提出了一套数据加密标准方案，简称DES。由于其密钥长度被设计成仅有56位，此方案一开始就被众多密码学家质疑其安全性。一九九八年EFF(电子前哨基金会)使用价值二万五千美元的并行计算机在大约九天的时间即能暴力破解DES，获得密钥。本节的重点并不是DES，而是DES采用的Feistel结构。

Feistel Network得名于德裔密码学家Horst Feistel，七十年代他在美国为IBM工作，DES方案采用了他和Don Coppersmith设计的加密结构。其示意图如下

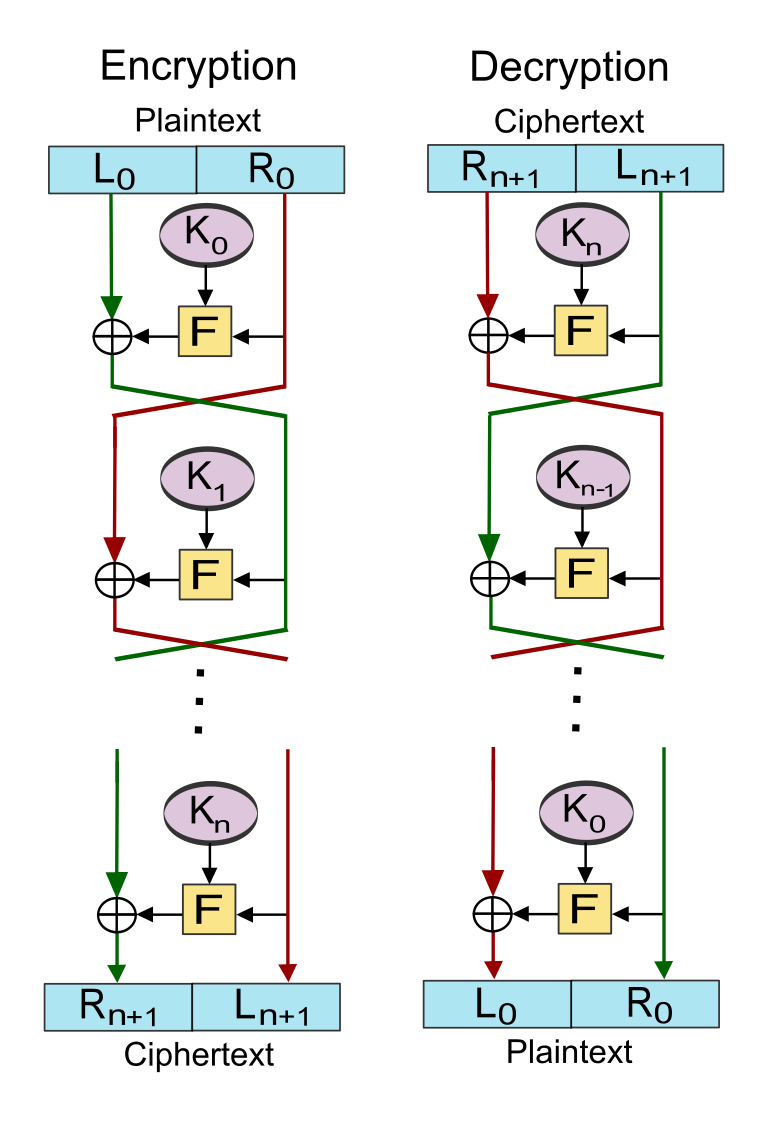
$$ L_{i+1} = R_i $$ $$ R_{i+1} = L_i \oplus F(R_i, K_i)$$ 其中\(i = 0, 1, \dots, n\)。

Feistel结构的优点是，加密函数F并不要求一定可逆。因为解密过程同加密一样，使用相同的结构，唯一区别就是子密钥的使用顺序完全相反，如上图右侧所示。可以这样做是因为一个特殊的运算XOR，它满足这样的性质\(a \oplus b = c \rightarrow a \oplus c = b, b \oplus c = a \)。所以我们有 $$ R_i = L_{i+1} $$ $$ L_i = R_{i+1} \oplus F(L_{i+1}, K_i)$$ 其中\(i = n, n-1, \dots, 0\)。

FEAL4

DES使用16轮加密函数，FEAL4仅使用了4轮加密函数。所以，尽管由纯软件实现，FEAL4的速度还是令人满意的。我们首先观察一下FEAL4的结构

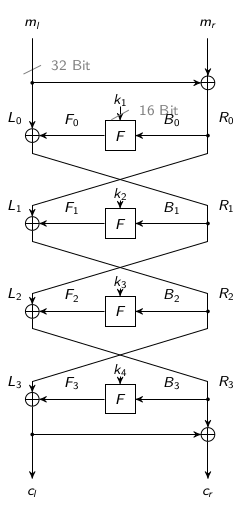
对FEAL4的线性分析的关键在F函数，在清水明宏和宫口庄司合著的论文¹里面，我们可以得到F函数的结构如图所示

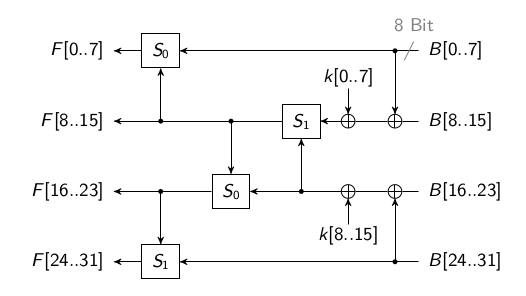
F函数的输入和输出被分成四部分，每部分8位，子密钥\(K_i\)被分成二个8位。在F函数里面存在二种S-Box，其计算定义如下 $$ S_i(a,b) = rot2(a + b + i \mod 256)$$

\(a, b\)为8位长数字，其值范围在[0,255]，\(i = 0, 1\)。\(rot2()\)是一个循环左移二位的操作，例如\(rot2(00000001) = 00000100\)。

线性分析

所谓线性分析，是为了寻找到加密系统的输入输出及密钥之间存在的线性依赖关系。有时候这种依赖关系仅仅在一定的概率上出现，但这也非常重要的信号，可能被攻击者加以利用。在上节分析F函数的时候，聪明的读者应该已经发现了一些线索。

正是由于S-Box的存在，攻击者可以找到F函数输入及输出之间的线性关系。我们再看 $$ S_0(a,b)[2] = a[0] \oplus b[0]$$ $$ S_1(a,b)[2] = a[0] \oplus b[0] \oplus 1$$

注意：这里的1仅仅在第〇位上才是确定存在的，更高位需要根据低位的进位情况才能决定是否+1。 结合F函数的结构，不难得到

$$ F[2] = B[0] \oplus F[8] $$ $$ F[10] = (B[0,8] \oplus K[0]) \oplus (B[16,24] \oplus K[8]) \oplus 1$$ $$ F[18] = F[8] \oplus (B[16,24] \oplus K[8])$$ $$ F[26] = F[16] \oplus B[24] \oplus 1$$

这就是F函数输入及输出间的线性关系。

前三轮

这四条线性关系可以扩展至首轮的输入与第三轮的输出之间，以第一条为例。在首轮有 $$ F_0[2] = B_0[0] \oplus F_0[8]$$

两边同时XOR \(F_0[8]\)得到 $$ \underline{F_0[2,8]} = B_0[0] = m_l[0] \oplus m_r[0]$$ 又有 $$ F_0[2,8] = \underline{L_0[2,8]} \oplus \underline{R_1[2,8]}$$ 其中 $$ L_0[2,8] = m_l[2,8]$$ $$ R_1[2,8] = L_2[2,8] = \underline{F_2[2,8]} \oplus R_3[2,8]$$ 在第三轮又有 $$ F_2[2,8] = B_2[0] = L_3[0]$$ 于是得到 $$ m_l[0,2,8] \oplus m_r[0] \oplus L_3[0] \oplus R_3[2,8] = 0$$

同理，利用第二条至第四条性质，继续得到

$$ m_l[0,8,10,16,24] \oplus m_r[0,8,16,24] \oplus L_3[0,8,16,24] \oplus R_3[10] = K_0[0,8] \oplus K_2[0,8] = 常数$$

$$ m_l[8,16,18,24] \oplus m_r[16,24] \oplus L_3[16,24] \oplus R_3[8,18] = K_0[8] \oplus K_2[8] = 常数$$ $$ m_l[16,24,26] \oplus m_r[24] \oplus L_3[24] \oplus R_3[16,26] = 0 $$

假设，攻击者已经获得了若干明文密文对，例如25对。利用这若干对明文和密文，和上述四条性质，攻击者可以很快确定可能的最后一个子密钥\(K_3\)。每个子密钥的空间为\(2^{16}\)，攻击者从0x0000开始遍尝\(K_3\)至0xffff， 首先有 $$ R_3 = c_l \oplus c_r $$

对密文\(c\)进行一次F计算 $$ L_3 = c_l \oplus F(R_3, K_3) $$

后三轮

同样的，可以找到第二轮的输入和末轮的输出之间的线性关系。还是以第一条性质为例，在末轮有 $$ \underline{F_3[2,8]} = R_3[0]$$

其中

$$ F_3[2,8] = c_l[2,8] \oplus \underline{L_3[2,8]}$$

根据FEAL4结构图得到

$$L_3[2,8] = \underline{F_1[2,8]} \oplus \underline{L_1[2,8]} $$

又有 $$ F_1[2,8] = R_1[0]$$ $$ L_1[2,8 = m_l[2,8] \oplus m_r[2,8]$$

所以得到

$$ m_l[2,8] \oplus m_r[2,8] \oplus c_l[0,2,8] \oplus c_r[0] \oplus R_1[0] = 0$$

同理，继续得到

$$ m_l[10] \oplus m_r[10] \oplus c_l[0,8,10,16,24] \oplus c_r[0,8,16,24] \oplus R_1[0,8,16,24] = 常数 $$ $$ m_l[8,18] \oplus m_r[8,18] \oplus c_l[8,16,18,24] \oplus c_r[16,24] \oplus R_1[16,24] = 常数$$ $$ m_l[16,26] \oplus m_r[16,26] \oplus c_l[16,24,26] \oplus c_r[24] \oplus R_1[24] = 0$$

这样，攻击者可以尝试获得子密钥\(K_0\)。同样在[0x0000, 0xffff]密钥空间内，攻击者尝试 $$ F_0 = F(m_l \oplus m_r, K_0)$$ $$ R_1 = m_l \oplus F_0$$

间两轮

$$ R_2 = L_1 \oplus F(R_1, K_1)$$ 并判断以下等式是否成立

$$ R_2 == L_3$$

结束语

笔者在对称加密这门课上学习了FEAL4的线性分析原理，并在实践课实现了此攻击方法。限于实验要求，最多只能使用25对明文密文，因此会出现不止一个\(K_3，K_0\)的情况。为了找到密钥，计算\(K_1,K_2\)时需要尝试所有的\(K_3,K_0\)的可能组合。这里是笔者实现攻击部分的代码，欢迎查看。