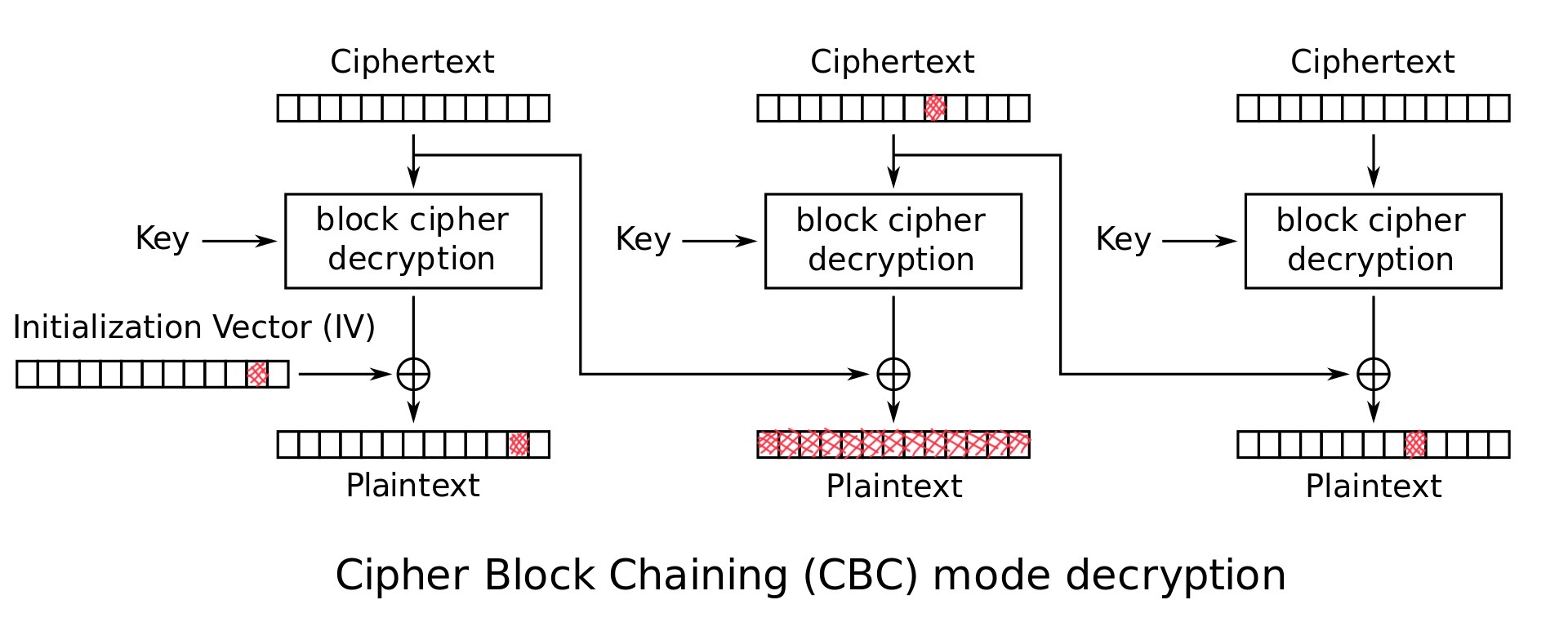
CBC(Cipher Block Chaining)是一种块加密,所谓块,就是一段固定长度的数据。明文,也就是待加密的数据,被分割成若干个块,然后分别加密每一个块。如果最后一个块未被填满,则需要额外的数据填充其中,然后加密。在本文首先介绍CBC加密系统的工作流程,然后就其采用的填充标准PKCS#7详细说明一种攻击方法。
CBC
首先看一下,CBC是如何加密
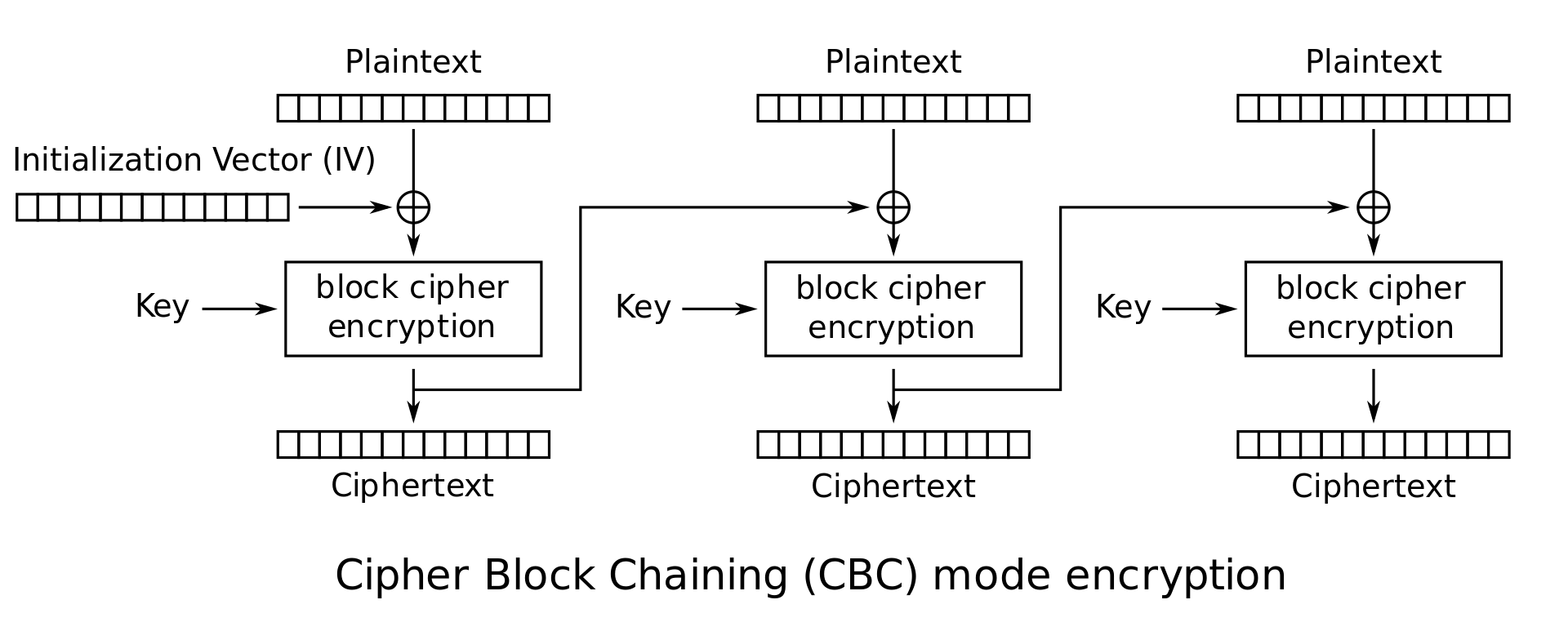
待加密的消息被分成若干个明文数据块,每个区块长度为\(L\),并按序编号为\(m_1,\cdots, m_n\)。明文\(m_i\)首先与前一个密文\(c_{i-1}\)进行一次异或操作XOR,运算结果进入加密函数得到密文\(c_i\)。其中,第一段明文\(m_1\)与一个随机选择的初始化向量\(IV\)异或。最终得到所有的密文区块\( C = (c_0=IV, c_1, \cdots, c_n)\),其中\(IV\)以明文传输。
CBC加密的数学形式为 $$ c_0 = IV,$$ $$ c_i = Enc_k(m_i \oplus c_{i-1})。$$
解密过程则与其相反
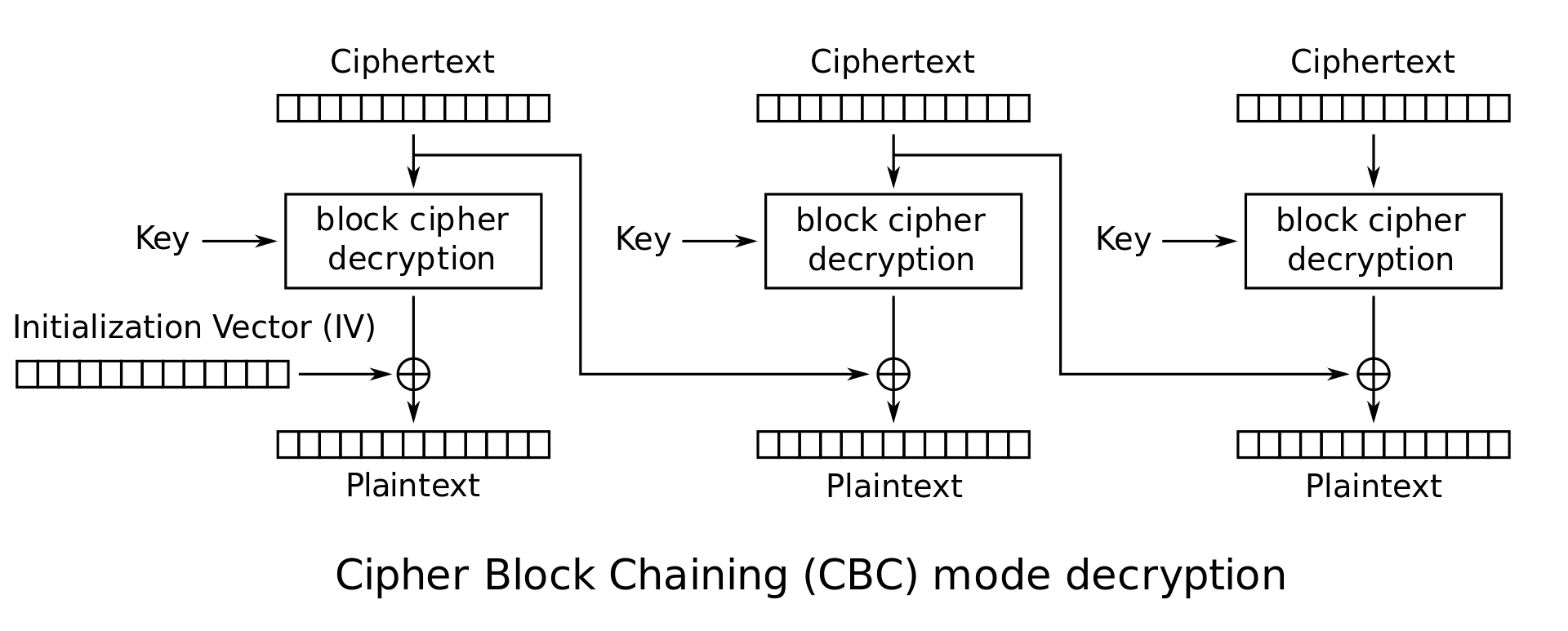
每段密文\(c_i\)首先被解密,然后与前一个密文\(c_{i-1}\)再异或得到明文\(m_i\)。 同样,简单地表达为 $$ c_0 = IV,$$ $$ m_i = Dec_k(c_i )\oplus c_{i-1}。$$
从示意图和表达式都很容易发现,每一个区块的加密或者解密都依赖于上一个区块的内容,这也是Block Chaining名称的由来。其中,解密过程可以并行计算,因为所有密文区块都是已知,而加密过程必须等待上一个密文区块计算完成。
比特翻转
在密文传输过程中,如果信道不稳定导致某个密文\(c_i\)中的一个比特位发生错误,比如因为宇宙射线的轰击,某个位上的1翻转成了0 🌚 解密的时候,因为解密函数运算会导致整个\(m_i\)损坏。同时,还会引起\(m_{i-1}\)的一位比特出现翻转错误,如上图红色部分所示。
而本文介绍的攻击方法正是基于密文比特翻转会引起下一块明文对应位置也会发生翻转的特性,下文会有详述。
PKCS#7
实际上,并不是所有的消息都能完整切割成几个块,总会有最后一个块长度不足的情况发生。此时,就需要填充额外的内容进去。假设一个区块的长度为L=16个字节,当最后一块内容长度不足时,根据PKCS#7规定,空余的每一个字节里填上的数值等于空余的字节数。例如
.. .. .. .. 30
-> .. .. .. .. 30 01
.. .. .. 30
-> .. .. .. 30 02 02
.. .. 30
-> .. .. 30 03 03 03
.. 30
-> .. 30 04 04 04 04
同样地,攻击者拥有一位Oracle,解密攻击者提交的密文并判断明文的填充是否符合标准,如是返回1,如否返回0。
攻击开始
有了Padding Oracle,攻击者可以恢复某个密文的明文。为了不至于文章太冗长,我们只演示对3个区块的攻击过程,其中第一个区块是初始化向量\(c_0 = IV\)。
先观察一下解密的过程,下图是一个简略的示意,帮助我们更直观地理解
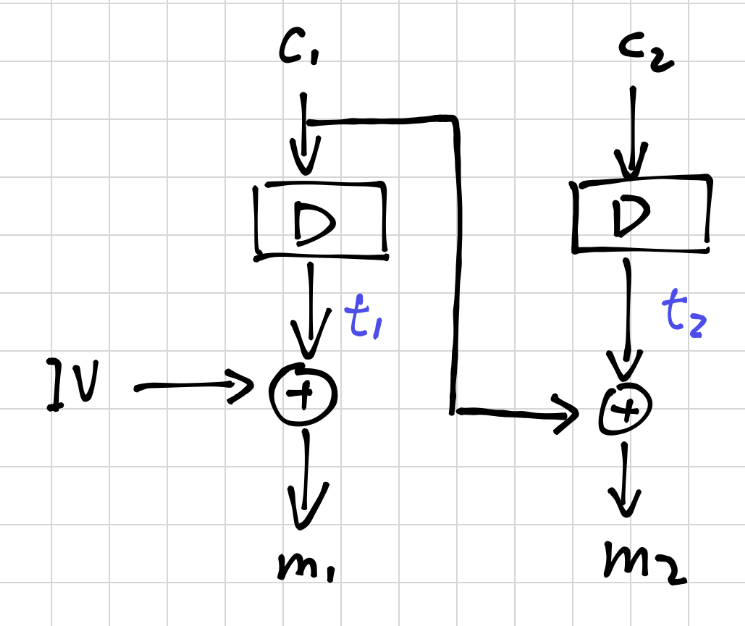
假设区块\(m_2\)被填充的长度为padding_len,则有
m_2[L-padding_len:L] == padding_len
为了确定明文的padding_len,攻击者从后往前,每次仅改动\(c_1\)的一个字节,其余内容保持原样,然后提交整个密文\(C = (IV,c_1,c_2)\)给Oracle解密。假如填充长度为3,也就意味着,头三次提交,Oracle返回值都为0,因为攻击者每次篡改,都导致了对应的填充区域内容发生改变。当攻击者第四次修改的时候,\(c_1\)的最后3个字节依然正确,也就意味着填充区域的内容合法,即03 03 03,此时Oracle返回1。如此,攻击者知道了填充区域的大小。正是这样逐字节修改\(c_1\)的内容,攻击最终能确定\(m_2\)的填充长度。
知道填充长度以后,该怎样恢复剩下的明文呢?这时候需要利用中间值:由上图可以知道\(t_2 = c_1 \oplus m_2\) ,此时攻击者已经知道明文的填充内容,因此他可以计算得到\(t_2\)对应区域的值
t_2[L-padding_len:L] = c_1[L-padding_len:L] ^ m_2[L-padding_len:L]
然后反过来他就可以精确改变填充内容\(m_2 = c_1 \oplus t_2\)。接着上例,攻击者现在想要使得填充内容为04,在对应的位置他只需要修改\(c_1 = 04 \oplus t_2\)
c_1[L-padding_len:L] = [04,04,04] ^ t_2[L-padding_len:L]
此时提交\(c_1\)被修改以后的密文给Oracle解密,基本上结果是0。因为此时明文的最后三个字节的填充内容变成了04 04 04,所以Oracle会继续往前检查一下字节,看是否为04。而从这里开始,就是消息的真正内容。而攻击者接下来要做就是,继续修改\(c_1\)里面这一字节的内容,然后提交Oracle解密,直到返回值为1。此时攻击者就知道了中间值对应位置的内容
padding_len = padding + 1
t_2[L-padding_len-1] = c_1[L-padding_len-1] ^ 04
m_2[L-padding_len-1] = c_1[L-padding_len-1] ^ t_2[L-padding_len-1]
如此这般不断修改填充部分的内容,增加填充长度,通过Orackle求出中间值,然后再和原始密文异或,最终能够恢复整个明文\(m_1,m_2\)。攻击者,胜。
结束语
此攻击的思路就是利用已知的填充内容和不停修改上一段密文,直到构造出一个合法的填充,求出当前密文(例如\(c_2\))对应的中间值,然后此中间值再和原始密文异或便得到明文。
上述攻击完成以后,攻击者就获得了一对明文密文\((M,C)\)。利用\((M,C)\)和Oracle攻击者甚至还能给任意一个明文\(M'\)构造一个合法的密文\(C'\)。思路类似,有兴趣的同学可以思考一下这是如何做到的?给一个小小的提示,以后有机会希望能够再写篇小文详细说明一番。
$$ IV’ = IV \oplus m_1 \oplus m’_1,\ c’_1 = c_1 $$
$$ m’_1 = Dec_k(c’_1) \oplus IV’ = Dec_k(c_1) \oplus IV \oplus m_1 \oplus m’_1$$
在笔者的代码里面,也实现了第一种和第二种攻击,欢迎查阅。