之前的小文详细介绍了如何利用Oracle实现对CBC的填充攻击,从而解出明文内容。此篇小文将解释如何利用这一对明文密文(m,c),在不知道密钥的情况下,构造一个对合法的明文密钥(M,C)。这样,攻击者便能在通信双方未能察觉之下修改通信内容,以达到自己的目的。跟前文一样,此文还是以二个消息块为例。有了前文的基础,此文直接进入主题。对CBC不了解或者不够熟悉的读者,请先翻阅前文。
消息区块二
为了方便理解,先放一张解密过程的简略示意图。
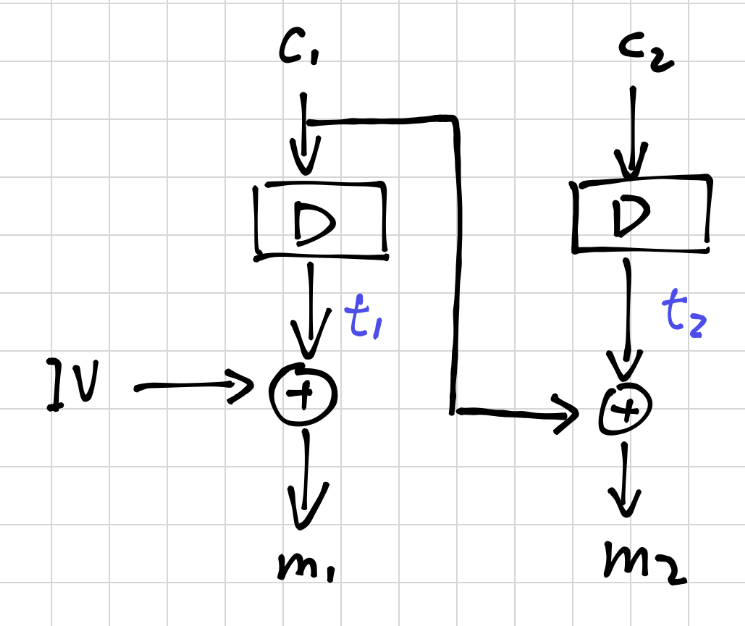
如前所述,攻击者此时已经获得一对(m,c),其中m=(m1,m2), c = (c1,c2)。现在攻击者希望给自己的消息M=(M1,M2)构造一个合法的密文C=(C1,C2),同样他需要来自Oracle的帮忙。
首先,对于消息区块M2,攻击者可以直接使用c2作为其密文C2 = c2。为了使解密过程合法,攻击者需要找到一个T2满足
$$ T2 = Dec_k(c2)$$
而T2又同时满足
$$ T2 = C1 \oplus M2$$
其中M2是攻击者想要传递的虚假消息,不能更改。所以只剩下C1可以动手
$$ C1 = Dec_k(c2) \oplus M2$$
c2源自攻击者已经获得的(m,c),所以
$$ Dec_k(c2) = c1 \oplus m2$$
于是 $$ C1 = c1 \oplus m2 \oplus M2$$
此时,对于第二个区块满足 $$ Dec_k(C2) \oplus C1 = Dec_k(c2) \oplus c1 \oplus m2 \oplus M2 = M2$$
即,解密过程合法。
消息区块一
当攻击者的区块二的明文和密文构造成功以后,区块一C1随即也被固定。对于第一个区块,有
$$ M1 = Dec_k(C1) \oplus IV$$
此时,攻击者能够自由选择内容的只剩下初始化向量IV,即攻击者必须找到一个IV满足上式。不难理解,只要求出\(Dec_k(C1)\)值,即T1,攻击者便得到
$$ IV = T1 \oplus M1$$
初始向量
CBC密文里IV的作用在于与消息区块一加密过后的结果T1进行XOR运算,能够自由选择IV内容,给了攻击者确定T1的机会。同样需要借助Oracle,攻击者提交(IV,C1)给Oracle,并根据反馈信息逐个字节修改IV直到得到一个合法的填充。具体过程如下:
先初始化IV = NULL,长度为L,填充长度padding_len = 1。然后从最末尾的字节开始修改,其取值范围是[0,255],攻击者尝试这256种可能,即IV = 000...00x,x = 0,...255。提交(IV, C1)至Oracle,当返回值为1时,由填充规则可知
T1[L-1] ^ x == 1
于是攻击者发现T1最后一个字节的值为T1[L-1] = x ^ 1。然后填充长度+1,并修改IV的最后一个字节
IV[L-1] = T1[L-1] ^ 2
接着尝试IV倒数第二个字节,并提交Oracle直到返回1。此时,
T1[L-2] ^ x == 2
如此,便又获得了T[L-2] = x ^ 2。填充长度+1,并修改
IV[L-2,L-1 ] = T1[L-2,L-1] ^ [3,3]
重复上述操作尝试获得T1[L-3]。如此持续下去,直到确定T[0],这样攻击者便完整获得了T1。于是
$$ IV = T1 \oplus M1 $$
满足
$$ Dec_k(C1) \oplus IV = T1 \oplus T1 \oplus M1 = M1$$
解密过程合法。
上述算法的代码片段如下所示,其中C[0:L-1] = IV, C[L,2*L-1] = C1
char oracle_rep;
unsigned char padding_len = 1;
unsigned char x;
unsigned char T1[L];
while (padding_len <= L)
{
x = 0;
while (x < 256)
{
C[L - padding_len] = x;
oracle_rep = padding_oracle(C);
if (oracle_rep == 1)
{
T1[L-padding_len] = x ^ padding_len;
padding_len++;
if (padding_len > L) break;
for (size_t i = 1; i < padding_len; i++)
{
C[L-i] = T1[L - i] ^ padding_len;
}
break;
}
x++;
}
}
这样,从已知的一对明密文(m,c),其中m=(m1,m2), c=(c1,c2)
攻击者便构造了一对合法的明文密文(M,C),满足
$$ C2 = c2$$ $$ C1 = c1 \oplus m2 \oplus M2$$ $$ IV = T1 \oplus M1 $$ $$ T1 = Dec_k(C1)$$