得益于无数聪明的头脑,对于区块链行业发展的思考和探索正在朝着两个方向迈进,有人在想象并期待着区块链之上能够出现更多安全而且可靠的DAPP,为数字资产的流动赋予无与伦比的自由和速度;也有人在深刻思索着区块链之下的共识机制,审视着人类协作活动的最基础性原理,以求得一条最为直接而且可信的通往共识之路,并改变人类组织的管理模式。
Poly Network是一个可实现在异构链之间转移资产的项目,研究共识机制是为了确保资产在不同区块链上的安全。接下来我们将用一系列的文章来介绍目前主流的共识算法,并尽可能解释清楚其运行的逻辑和背后的博弈原理。同时,在认真对比这些算法之后,Poly Network也能够从前人的研究中获得启发,寻找到更匹配自身发展要求的共识机制。
以下内容将是本系列的第一篇文章,让我们从分布式系统的基本困境开始谈起。
CAP不可能三角
在计算机发展史的古早时期,大型主机优异的计算性能引起了政府、金融和电信部门的兴趣,可一旦主机出现了问题无法工作,整个系统将出于不可用状态,部门的业务也随之瘫痪。随着可靠又稳定的通信网络出现,多机系统渐渐变成现实,不同机器之间互相合作,互为备份,构成分布式系统,从而规避前述的「单点故障」难题。然而,分布式系统也有自己的难题需要处理。
分布式系统是一个硬件或软件组件分布在不同的网络计算机之上,彼此之间仅仅通过消息传递来进行通信和协调的系统。
— 《分布式系统概念与设计》
在比特币面世之前,计算机科学家们已经对分布式系统进行了几十年的细致研究,并证明了CAP不可能定理,指出对于一个分布式计算系统来说,不可能同时满足一下三个性质
- 一致性(Consistency) ,即所有客户访问同一份最新数据的副本
- 可用性(Aailability),即客户的每次请求都能获得响应,但不保证响应数据是最新的
- 分区容错性(Partition tolerance),即系统在时限内未能达成数据的一致性,发生了分区,意味着不同分区的最新数据不一致
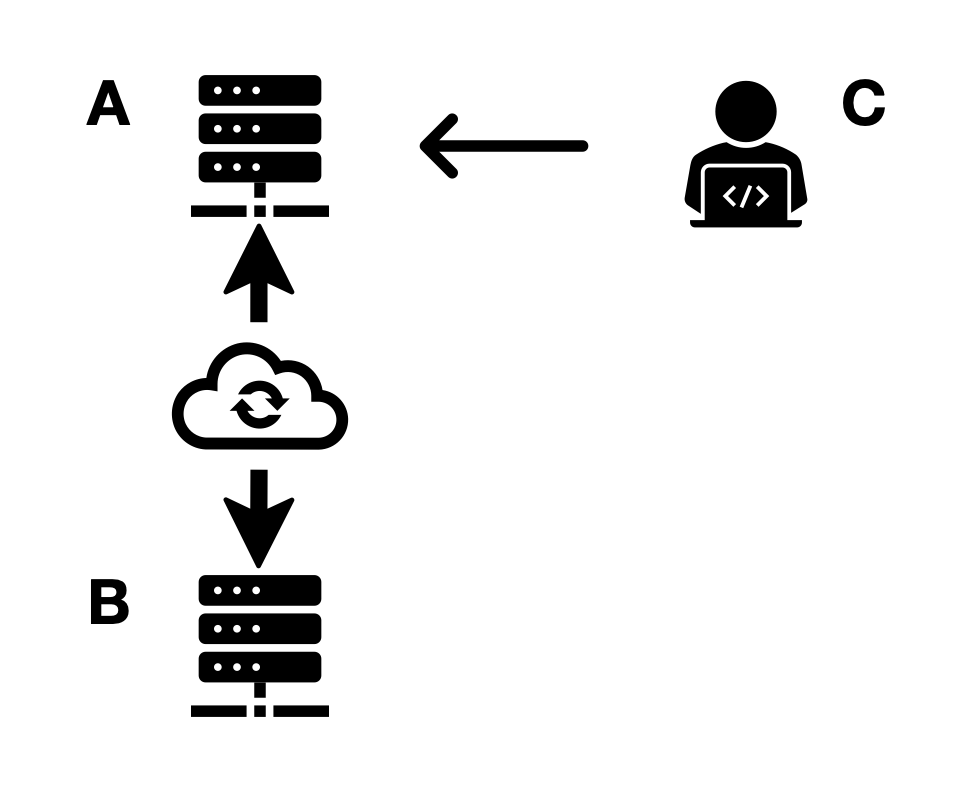
我们设置一个最简单的分布式系统模型来进一步解释,该模型包含两个节点A和B,假设此时节点A和B的数据库完全一致,并且客户C在之后某一时刻访问了节点A并且对数据库发起了写操作。于是,节点A和B的数据库不再一致,即系统出现了分区(满足分区容错性)。在剩下的两个性质中,最多只能再满足一个:为了确保一致性,节点B不能再被访问;若要保证可用性,则自动丧失了数据的一致性。
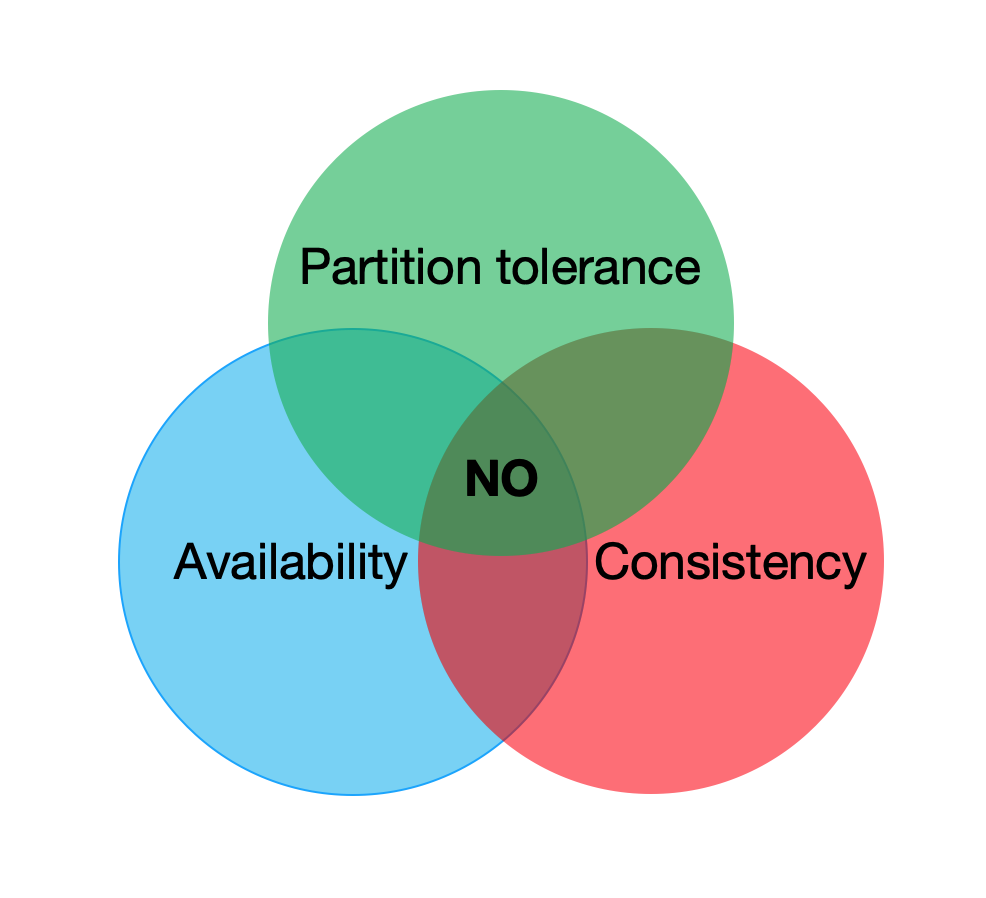
上图就是著名的CAP不可能三角,它就像热力学第二定律一样,令分布式系统的设计者感到绝望,如今的区块链行业也受困于此。
拜占庭将军问题
远在CAP定理被证明之前的二十年,即1982年,计算机科学家 Lamport 为了解决分布式系统中的数据一致性,提出了拜占庭将军问题(Byzentine Generals Problem)。
敌国的城市被几支拜占庭军队团团围困住,每支军队由一名将军统帅,他们依靠行动迅捷的信使来传递消息,以达成一致的行动,即进攻或者撤退,只要超过半数将军的同意才能决定最终行动。
初看,似乎这是一个很简单的问题,其实魔鬼藏在细节里面。信使能否及时将消息传达至目的军营,消息有没有被信使篡改,最严重的担心是将军里面会不会出现叛徒,发布错误消息。这些现实的担忧都会影响最终一致性的达成,从而导致行动失败。借助现代通信系统的低时延和稳定性,第一个问题被漂亮地解决,密码学家发明的加密算法和数字签名又优雅地解决了第二个问题。而第三个问题本质上是信任问题,也是今天区块链想要为世界解决的难题。
拜占庭的将军们需要一种共识算法来保证
A. 所有忠诚的将军最终采取相同行动
B. 叛徒不会误导忠诚的将军采取错误的行动
为了更好地描述共识过程,约定以下符号
- $n$:将军数量
- $v_i$: 将军 $i$ 向其他将军发送的消息
- $V_i={v_1, v_2, …, v_n }$:将军 $i$ 收集的其他将军的消息和自己的消息的集合
- $Majority(V_i)$:将军 $i$ 根据消息集合中的多数意见所作出的行动
将军之间若要达成一致行动,需要每位将军告诉其他所有将军自己的意见。假设将军 $i$ 是忠诚的,则断定达成共识的每一个忠诚将军的消息集合 $V$ 中 $v_i$ 相同,并且每一个忠诚的将军会如实转发其他将军的消息,这暗示其他将军不一定是从将军 $i$ 处直接获得 $v_i$;叛徒 $j$ 会向不同的将军发送不同的指令 $v_j$,并且会向其他将军转发被篡改的 $v_i$。
保证A和B成立,共识算法必须满足
条件1. 每个忠诚将军必须获得相同的消息集合 $V$
条件2. 如果将军 $i$ 是忠诚的,则每个忠诚将军的消息集合 $V_i$ 必须包含正确的$v_i$
在拜占庭模型中,一定能达成共识的忠诚将军数量最少是3。接下来将说明,只要存在1个叛徒,剩下2个将军无法达成一致行动。如下图所示,三位拜占庭将军包围了敌城,但是将军G3临阵倒戈,成为叛徒,意图干扰剩下二位将军的行动。
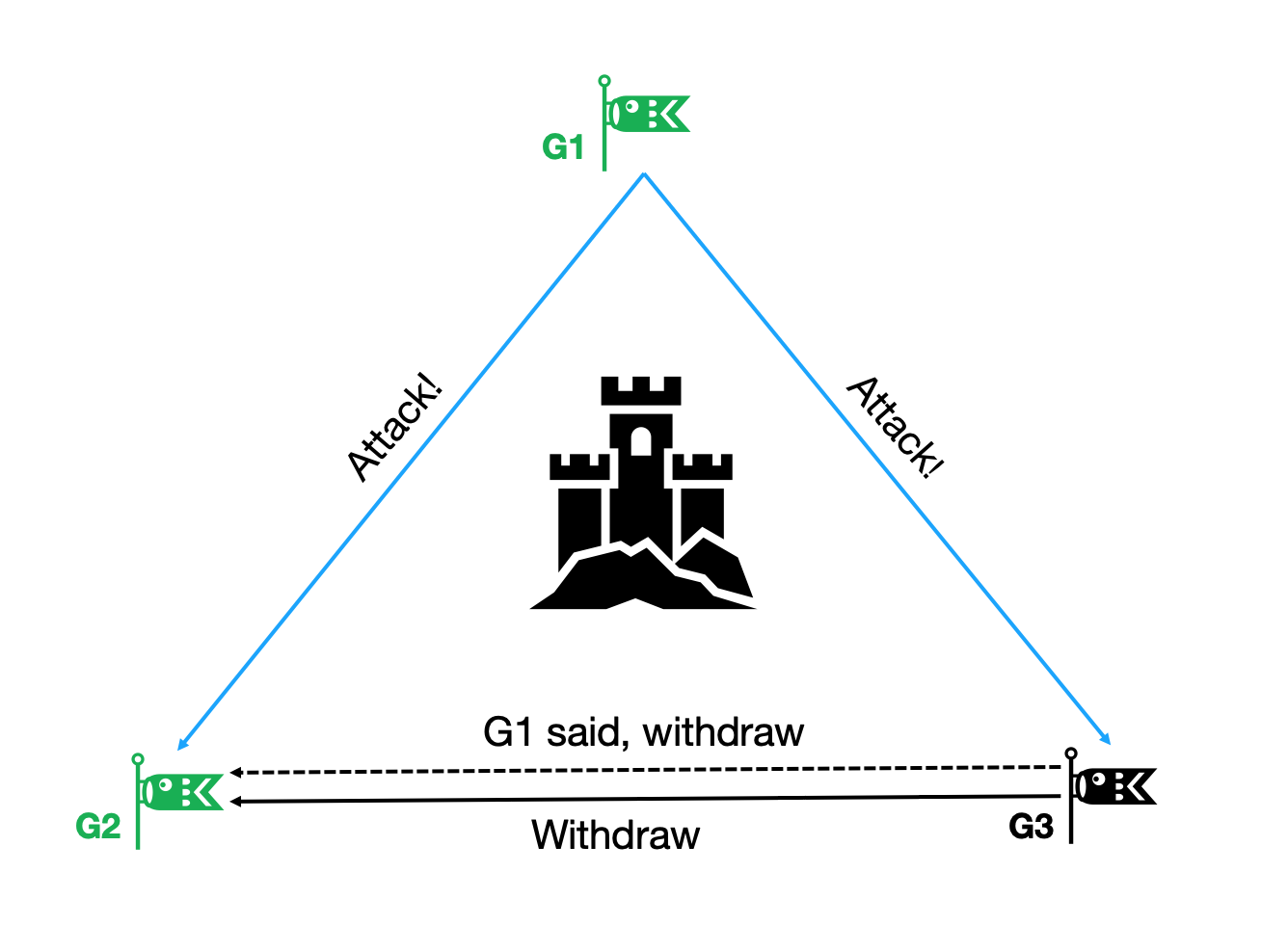
将军 G1 决意攻城,于是向剩下的二位将军发送「进攻」指令 $v_1$,将军 G2 收到指令后等待来自 G3 的消息。叛徒 G3 为了阻止攻城,发送「撤退」指令 $v_2$,并且篡改 G1 的消息为「撤退」指令 $v_{1’}$,然后向 G2 转发。此时 G1 接到来自 G3 的「撤退」指令 $v_3$,等待来自 G2 的消息才能确定最终行动。忠诚将军 G2 收到 $v_3$ 并同时收到了一条与 $v_1$ 相反的指令 $v_{1’}$,此时他无法判断哪一条指令真正来自 G1,同时也不能根据 $v_1$ 和 $v_3$ 作出「进攻」的决定,无法与G1达成共识,不满足性质A和性质B。如果此时有另外一名忠诚的将军 G4 转发指令 $v_1$ 给 G2,后者就能判断出 G1 的真实意图,从而根据$Majority(V_2)$ 得出正确的行动指令。
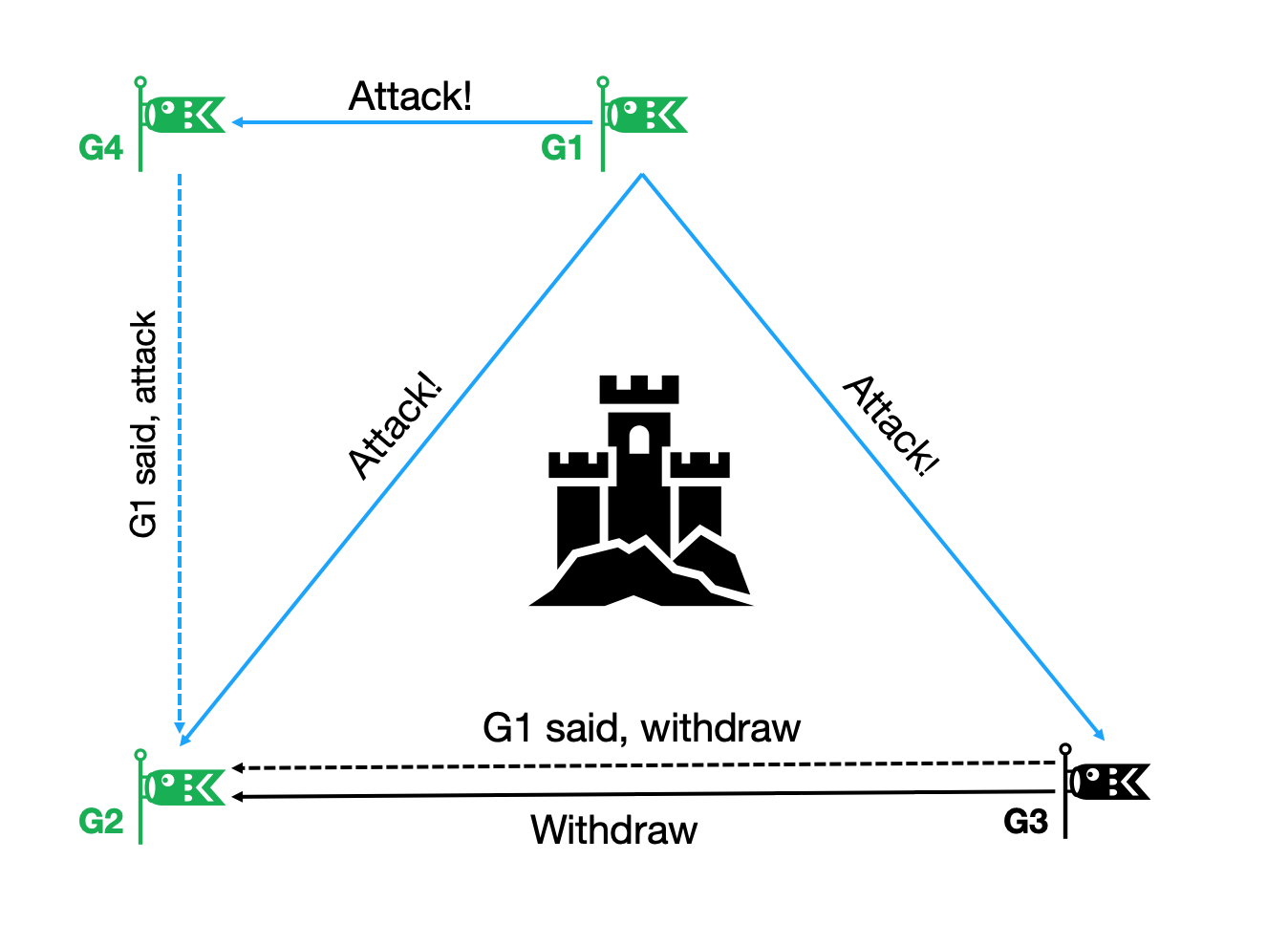
同样的道理,假如现在有 $3m$ 位将军,其中三分之一,即 $m$ 个叛徒,只要它们共谋捣乱,就会干扰剩下的三分之二,即 $2m$ 位将军无法达成一致行动。此时只需要再多一位忠诚将军,就能帮助完成共识。
这就是Lamport为解决数据一致性提出来的模型:在一个分布式系统中,最多能够容忍的作恶节点数量必须小于总数的三分之一,诚实节点之间才有可能达成共识,否则无解。
在拜占庭模型提出来之后的若干年,计算机科学家继续为此模型设计了不同的算法,用来确保系统能够高效可信地达成共识,其中第一个被广泛认可的算法是由 Liskov 和 Castro 在1999年提出来的实用拜占庭容错算法(Practical Byzantine Fault Tolerance, pBFT),将在下一篇文章中详细介绍,请期待。